Integers
In this chapter you will work with whole numbers smaller than 0. These numbers are called negative numbers. The whole numbers larger than 0, 0 itself and the negative whole numbers together are called the integers. Mathematicians have agreed that negative numbers should have certain properties that would make them useful for various purposes. You will learn about these properties and how they make it possible to do calculations with negative numbers.

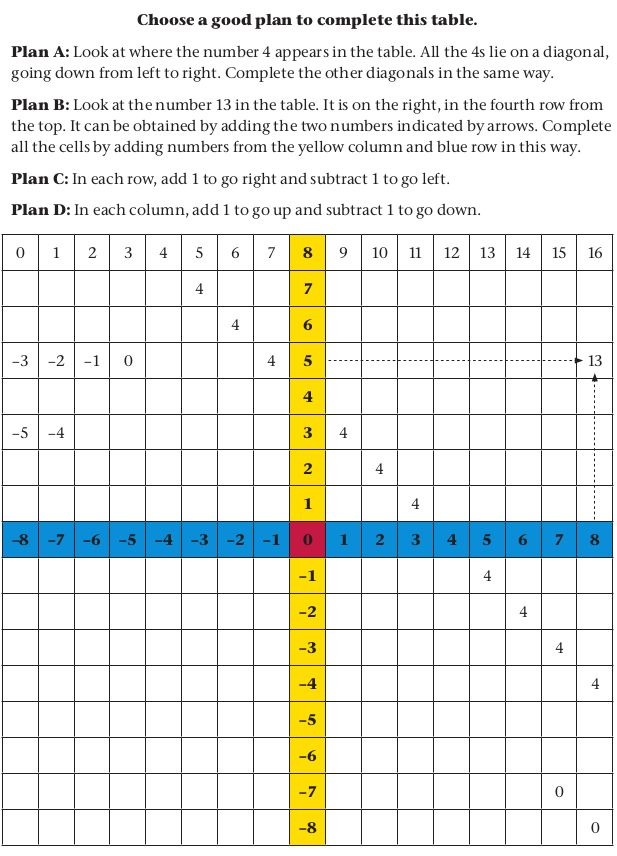
What is beyond
Why people decided to have negative numbers
Below, you can see how Jimmy prefers to work when doing calculations such as 542 + 253.
\(500 + 200 = 700 \\ 40 + 50 = 90 \\ 2 + 3 = 5 \\ 700 + 90 + 5 = 795\)
He tries to calculate 542 - 253 in a similar way:
\( \begin{align} 500 - 200 &= 300 \\ 40 - 50 &= ? \end{align} \)
Jimmy clearly has a problem. He reasons as follows:
I can subtract 40 from 40; that gives 0. But then there is still 10 that I have to subtract.
He decides to deal with the 10 that he still has to subtract later, and continues:
\( \begin{align} 500 - 200 &= 300 \\ 40 - 50 &= 0 \textit{, but there is still 10 that I have to subtract.} \\ 2 - 3 &= 0 \textit{, but there is still 1 that I have to subtract.} \end{align} \)
-
- What must Jimmy still subtract, and what will his final answer be?
- When Jimmy did another subtraction problem, he ended up with this writing at one stage:
600 and (-)50 and (-)7
What do you think is Jimmy's final answer for this subtraction problem?
- What must Jimmy still subtract, and what will his final answer be?
About 500 years ago, some mathematicians proposed that a "negative number" may be used to describe the result in a situation such as in Jimmy's subtraction problem above, where a number is subtracted from a number smaller than itself.
For example, we may say \(10 - 20 = (-10)\)
This proposal was soon accepted by other mathematicians, and it is now used all over the world.
Mathematicians are people who do mathematics for a living. Mathematics is their profession, like health care is the profession of nurses and medical doctors.
- Calculate each of the following:
- \( 16 - 20\)
- \( 16 - 30\)
- \( 16 - 40\)
- \( 16 - 60\)
- \( 16 - 200\)
- \( 5 - 1 000\)
- \( 16 - 20\)
- Some numbers are shown on the lines below. Fill in the missing numbers.
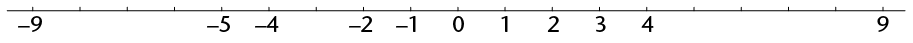
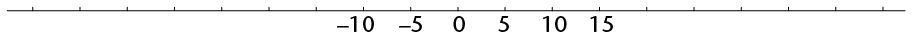
The numbers 1; 2; 3; 4 etc. are called the natural numbers. The natural numbers, 0 and the negative whole numbers together are called the integers.
The following statement is true if the number is 5:
15 - (a certain number) = 10
A few centuries ago, some mathematicians decided they wanted to have numbers that will also make sentences like the following true:
15 + (a certain number) = 10
But to go from 15 to 10 you have to subtract 5.
The number we need to make the sentence 15 + (a certain number) = 10 true must have the following strange property:
If you add this number, it should have the same effect as to subtract 5.
Now the mathematicians of a few centuries ago really wanted to have numbers for which such strange sentences would be true. So they thought:
Let us decide, and agree amongst ourselves, that the number we call negative 5 will have the property that if you add it to another number, the effect will be the same as when you subtract the natural number 5.
This means that the mathematicians agreed that \( 15 + (-5)\) is equal to \(15 - 5\).
Stated differently, instead of adding negative 5 to a number, you may subtract 5.
Adding a negative number has the same effect as subtracting a natural number.
For example: \(20 + (-15) = 20 - 15 = 5\)
- Calculate each of the following:
- \(500 + (-300)\)
- \(100 + (-20) + (-40)\)
- \(500 + (-200) + (-100)\)
- \( 100 + (-60)\)
- \(500 + (-300)\)
- Make a suggestion of what the
answer for \((-20) + (-40) \) should be. Give reasons for your suggestion.
- Continue the lists of numbers below to complete the table.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
10
100
3
-3
-20
150
0
9
90
6
-6
-18
125
-5
8
80
9
-9
-16
100
-10
7
70
12
-12
-14
75
-15
6
60
15
-15
50
-20
5
50
-25
4
40
3
30
2
20
1
10
-1
-10
The following statement is true if the number is 5:
15 + (a certain number) = 20
What properties should a number have so that it makes the following statement true?
15 - (a certain number) = 20
To go from 15 to 20 you have to add 5. The number we need to make the sentence 15 - (a certain number) = 20 true must have the following property:
If you subtract this number, it should have the same effect as to add 5.
Let us agree that \( 15 - (-5) \) is equal to \(15 + 5\).
Stated differently, instead of subtracting negative 5 from a number, you may add 5.
Subtracting a negative number has the same effect as adding a natural number.
For example: \(20 - (-15) = 20 + 15 = 35\)
- Calculate.
- \(30 - (-10)\)
- \(30 + 10\)
- \(30 + (-10)\)
- \(30 - 10\)
- \(30 - (-30)\)
- \(30 + 30\)
- \(30 + (-30)\)
- \(30 - 30\)
- \(30 - (-10)\)
You probably agree that
\[ \begin{align} 5 + (-5) &= 0 \\ 10 + (-10) &= 0 \\ \text{and} \\ 20 + (-20) &= 0 \end{align} \]
We may say that for each "positive" number there is a corresponding or opposite negative number. Two positive and negative numbers that correspond, for example 3 and (-3), are called additive inverses. They wipe each other out when you add them.
What may each of the following be equal to?
\((-8) + 5\)
\((-5) + (-8)\)
When you add any number to its additive inverse, the answer is 0 (the additive property of 0). For example, \( 120 + (-120) = 0\).
- Write the additive inverse of each of the following numbers:
- 24
- -24
- -103
- 2 348
- 24
The idea of additive inverses may be used to explain why \(8 + (-5)\) is equal to 3:
\[8 + (-5) = 3 + \boxed{5 + (-5)} = 3 + 0 = 3 \]
- Use the idea of additive inverses to explain why each of these statements is true:
- \( 43 + (-30) = 13 \)
- \(150 + (-80) = 70 \)
- \( 43 + (-30) = 13 \)
Statements that are true for many different numbers
For how many different pairs of numbers can the following statement be true, if only natural (positive) numbers are allowed?
a number + another number = 10
For how many different pairs of numbers can the statement be true if negative numbers are also allowed?
Adding and subtracting with integers
Adding can make less and subtraction can make more
- Calculate each of the following:
- \(10 + 4 + (-4)\)
- \(10 + (-4) + 4\)
- \(3 + 8 + (-8)\)
- \(3 + (-8) + 8\)
- \(10 + 4 + (-4)\)
The numbers 1; 2; 3; 4; etc. that we use to count, are called natural numbers.
Natural numbers can be arranged in any order to add and subtract them. This is also the case for integers.
- Calculate each of the following:
- \(18 + 12\)
- \(12 + 18\)
- \( 2 + 4 + 6\)
- \(6 + 4 + 2\)
- \(2 + 6 + 4\)
- \(4 + 2 + 6\)
- \( 4 + 6 + 2\)
- \( 6 + 2 + 4\)
- \( 6 + (-2) + 4\)
- \( 4 + 6 + (-2)\)
- \(4 + (-2) + 6\)
- \( (-2) + 4 + 6\)
- \( 6 + 4 + (-2)\)
- \( (-2) + 6 + 4\)
- \( (-6) + 4 + 2\)
- \(18 + 12\)
- Calculate each of the following:
- \( (-5) + 10\)
- \( 10 + (-5)\)
- \( (-8) + 20\)
- \( 20 - 8\)
- \( 30 + (-10)\)
- \(30 + (-20)\)
- \(30 + (-30)\)
- \( 10 + (-5) + (-3)\)
- \((-5) + 7 + (-3) + 5\)
- \( (-5) + 2 + (-7) + 4\)
- \( (-5) + 10\)
- In each case, find the number
that makes the statement true. Give your answer by writing a closed number
sentence.
- 20 + (an unknown number) = 50
- 50 + (an unknown number) = 20
- 20 + (an unknown number) = 10
- (an unknown number) + (-25) = 50
- (an unknown number) + (-25) = -50
- 20 + (an unknown number) = 50
Statements like these are also called number sentences.
An incomplete number sentence, where some numbers are not known at first, is sometimes called an open number sentence:
8 - (a number) = 10
A closed number sentence is where all the numbers are known:
\(8 + 2 = 10\)
- Use the idea of additive inverses to explain why each of the following statements is true:
- \( 43 + (-50) = -7\)
- \( 60+ (-85) = -25 \)
- \( 43 + (-50) = -7\)
- Complete the table as far as you can.
(a)
(b)
(c)
\(5 - 8 = \)
\(5 + 8 = \)
\(8 - 3 = \)
\(5 - 7 =\)
\(5 + 7 =\)
\(7 - 3 =\)
\(5 - 6 =\)
\(5 + 6 =\)
\(6 - 3 =\)
\(5 - 5 =\)
\(5 + 5 =\)
\(5 - 3 =\)
\(5 - 4 =\)
\(5 + 4 =\)
\(4 - 3 =\)
\(5 - 3 =\)
\(5 + 3 =\)
\(3 - 3 =\)
\(5 - 2 =\)
\(5 + 2 =\)
\(2 - 3 =\)
\(5 - 1 =\)
\(5 + 1 =\)
\(1 - 3 =\)
\(5 - 0 =\)
\(5 + 0 =\)
\(0 - 3 =\)
\(5 - (-1) =\)
\(5 + (-1) =\)
\((-1) - 3 =\)
\(5 - (-2) =\)
\(5 + (-2) =\)
\((-2) - 3 =\)
\(5 - (-3) =\)
\(5 + (-3) =\)
\((-3) - 3 =\)
\(5 - (-4) =\)
\(5 + (-4) =\)
\((-4) - 3 =\)
\(5 - (-5) =\)
\(5 + (-5) =\)
\((-5) - 3 =\)
\(5 - (-6) =\)
\(5 + (-6) =\)
\((-6) - 3 =\)
- Calculate.
- \(80 + (-60)\)
- \(500 + (-200) + (-200)\)
- \(80 + (-60)\)
-
- Is \(100 + (-20) + (-20) = 60\), or does it equal something else?
- What do you think \((-20) + (-20)\) is equal to?
- Is \(100 + (-20) + (-20) = 60\), or does it equal something else?
- Calculate.
- \(20 - 20\)
- \(50 - 20\)
- \( (-20) - (-20)\)
- \((-50) - (-20)\)
- \(20 - 20\)
- Calculate.
- \( 20 - (-10)\)
- \( 100 - (-100)\)
- \( 20 + (-10)\)
- \(100 + (-100)\)
- \((-20) - (-10)\)
- \( (-100) - (-100)\)
- \( (-20) + (-10)\)
- \( (-100) + (-100)\)
- \( 20 - (-10)\)
- Complete the table as far as you can.
(a)
(b)
(c)
\( 5 - (-8) \) =
\( (-5) + 8 =\)
\( 8 - (-3) =\)
\( 5 - (-7) =\)
\( (-5) + 7 =\)
\( 7 - (-3) =\)
\( 5 - (-6) =\)
\( (-5) + 6 =\)
\( 6 - (-3) =\)
\( 5 - (-5) =\)
\( (-5) + 5 = \)
\( 5 - (-3) =\)
\( 5 - (-4) =\)
\( (-5) + 4 =\)
\( 4 - (-3) =\)
\( 5 - (-3) =\)
\( (-5) + 3 =\)
\( 3 - (-3) =\)
\( 5 - (-2) =\)
\( (-5) + 2 =\)
\( 2 - (-3) =\)
\( 5 - (-1) =\)
\( (-5) + 1 =\)
\( 1 - (-3) =\)
\( 5 - 0 =\)
\( (-5) + 0 =\)
\( 0 - (-3) =\)
\( 5 - 1 =\)
\( (-5) + (-1) =\)
\( (-1) - (-3) =\)
\( 5 - 2 =\)
\( (-5) + (-2) =\)
\( (-2) - (-3) =\)
\( 5 - 3 = \)
\( (-5) + (-3) = \)
\( (-3) - (-3) = \)
\( 5 - 4 = \)
\( (-5) + (-4) = \)
\( (-4) - (-3) = \)
\( 5 - 5 = \)
\( (-5) + (-5) = - \)
\((-5) - (-3) = \)
- In each case, state whether the statement is true or false and give a numerical example to demonstrate your answer.
- Subtracting a positive number from a negative number has the same effect as dding the additive inverse of the positive number.
- Adding a negative number to a positive number has the same effect as adding the additive inverse of the negative number.
- Subtracting a negative number from a positive number has the same effect as subtracting the additive inverse of the negative number.
- Adding a negative number to a positive number has the same effect as subtracting the additive inverse of the negative number.
- Adding a positive number to a negative number has the same effect as adding the additive inverse of the positive number.
- Adding a positive number to a negative number has the same effect as subtracting the additive inverse of the positive number.
- Subtracting a positive number from a negative number has the same effect as subtracting the additive inverse of the positive number.
- Subtracting a negative number from a positive number has the same effect as adding the additive inverse of the negative number.
- Subtracting a positive number from a negative number has the same effect as dding the additive inverse of the positive number.
Comparing integers and solving problems
- Fill <, > or = into the block to make the relationship between the numbers true:
- -103 ☐ -99
- -699 ☐ -701
- 30 ☐ -30
- 10-7 ☐ -(10-7)
- -121 ☐ -200
- -12 - 5 ☐ -(12 + 5)
- -199 ☐ -110
- At 5 a.m. in Bloemfontein the temperature was -5 °C. At 1 p.m., it was 19 °C. By how many degrees did the temperature rise?
- A diver swims 150 m below the surface of the sea. She moves 75 m towards the surface. How far below the surface is she now?
- One trench in the ocean is 800 m deep and another is 2 200 m deep. What is the difference in their depths?
- An island has a mountain which is 1 200 m high. The surrounding ocean has a depth of 860 m. What is the difference in height?
- On a winter's day in Upington the temperature rose by 19 °C. If the minimum temperature was -4 °C, what was the maximum temperature?
Multiplying and dividing with integers
Multiplication with integers
- Calculate.
- \( -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5\)
- \( -10 + -10 + -10 + -10 + -10\)
- \( -6 + -6 + -6 + -6 + -6 + -6 + -6 + -6\)
- \( -8 + -8 + -8 + -8 + -8 + -8\)
- \( -20 + -20 + -20 + -20 + -20 + -20 + -20\)
- \( -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5 + -5\)
- In each case, show whether you agree (â) or disagree (â) with the given statement.
- \( 10 \times (-5) = 50\)
- \( 8 \times (-6) = (-8) \times 6\)
- \( (-5) \times 10 = 5 \times (-10)\)
- \( 6 \times (-8) = -48\)
- \( (-5) \times 10 = 10 \times (-5)\)
- \( 8 \times (-6) = 48\)
- \( 4 \times 12 = -48\)
- \( (-4) \times 12 = -48\)
- \( 10 \times (-5) = 50\)
Multiplication of integers is commutative:
\((-20) \times 5 = 5 \times (-20)\)
- Is addition of integers commutative? Demonstrate your answer with three different examples.
- Calculate.
- \(20 \times (-10)\)
- \((-5) \times 4\)
- \((-20) \times 10\)
- \(4 \times (-25)\)
- \(29 \times (-20)\)
- \((-29) \times (-2)\)
- \(20 \times (-10)\)
- Calculate.
- \( 10 \times 50 + 10 \times (-30)\)
- \( 50 + (-30)\)
- \(10 \times {\bf(}50 + (-30){\bf)}\)
- \((-50) + (-30) \)
- \(10 \times (-50) + 10 \times (-30) \)
- \(10 \times {\bf(}(-50) + (-30){\bf)} \)
- \( 10 \times 50 + 10 \times (-30)\)
The product of two positive numbers is a positive number, for example \(5 \times 6 = 30\).
The product of a positive number and a negative number is a negative number, for example \(5 \times (-6) = -30\).
The product of a negative number and a positive number is a negative number, for example \( (-5) \times 6 = -30\).
-
- Four numerical expressions are given below. Underline the expressions that you would expect to have the same answers. Do not do the calculations.
\[14 \times (23 + 58) \\ 23 \times (14 + 58) \\ 14 \times 23 + 14 \times 58 \\ 14 \times 23 + 58\]
- What property of operations is demonstrated by the fact that two of the above expressions have the same value?
- Four numerical expressions are given below. Underline the expressions that you would expect to have the same answers. Do not do the calculations.
- Consider your answers for question 6.
- Does multiplication distribute over addition in the case of integers?
- Illustrate your answer with two examples.
- Does multiplication distribute over addition in the case of integers?
- Three numerical expressions are given below. Underline the expressions that you would expect to have the same answers. Do not do the calculations.
\[10 \times {\bf(}(-50) - (-30){\bf)} \\ 10 \times (-50) - (-30) \\ 10 \times (-50) - 10 \times (-30) \]
- Do the three sets ofcalculations given in question 8.
Your work in questions 5, 8 and 9 demonstrates that multiplication with a positive number distributes over addition and subtraction of integers. For example:
\[ 10 \times {\bf(}5 + (-3){\bf)} = 10 \times 2 = {\bf20} \text{ and } 10 \times 5 + 10 \times (-3) = 50 + (-30) = {\bf 20} \]
\[ 10 \times {\bf(}5 - (-3){\bf)} = 10 \times 8 = {\bf 80} \text{ and } 10 \times 5 - 10 \times (-3) = 50 - (-30) = {\bf 80} \]
- Calculate: \((-10) \times {\bf(}5 + (-3){\bf)} \)
Now consider the question of whether multiplication with a negative number distributes over addition and subtraction of integers. For example, would \((-10) \times 5 + (-10) \times (-3)\) also have the answer -20, as does \((-10) \times {\bf(}5 + (-3){\bf)}\)?
- What must \((-10) \times (-3)\) be equal to, if we want \((-10) \times 5 + (-10) \times (-3)\) to be equal to -20?
In order to ensure that multiplication distributes over addition and subtraction in the system of integers, we have to agree that
(a negative number) \(\times\) (a negative number) is a positive number,
for example \((-10) \times (-3) = 30\).
- Calculate.
- \((-10) \times (-5)\)
- \((-10) \times 5\)
- \(10 \times 5\)
- \(10 \times (-5)\)
- \((-20) \times (-10) + (-20) \times (-6)\)
- \((-20) \times {\bf(}(-10) + (-6){\bf)}]\)
- \((-20) \times (-10) - (-20) \times (-6)\)
- \((-20) \times {\bf(}(-10) - (-6){\bf)}\)
- \((-10) \times (-5)\)
Here is a summary of the properties of integers that make it possible to do calculations with integers:
- When a number is added to its additive inverse, the result is 0, for example \( (+12) + (-12) = 0\).
- Adding an integer has the same effect as subtracting its additive inverse. For example, \( 3 + (-10)\) can be calculated by doing \(3 - 10\), and the answer is -7.
- Subtracting an integer has the same effect as adding its additive inverse. For example, \( 3 - (-10)\) can be calculated by doing \(3 + 10\), and the answer is 13.
- The product of a positive and a negative integer is negative, for example \( (-15) \times 6 = -90\).
- The product of a negative and a negative integer is positive, for example \( (-15) \times (-6) = 90\).
Division with integers
-
- Calculate \(25 \times 8\).
- How much is \( 200 \div 25?\)
- How much is \( 200 \div 8?\)
- Calculate \(25 \times 8\).
Division is the inverse of multiplication. Hence, if two numbers and the value of their product are known, the answers to two division problems are also known.
- Calculate.
- \(25 \times\ (-8) )\)
- \((-125) \times 8\)
- \(25 \times\ (-8) )\)
- Use the work you have done for question 2 to write the answers for the following division questions:
- \( (-1 000) \div (-125)\)
- \( (-1 000) \div 8\)
- \( (-200) \div 25\)
- \( (-200) \div 8\)
- \( (-1 000) \div (-125)\)
- Can you also work out the answers for the following division questions by using the work you have done for question 2?
- \( 1 000 \div (-125)\)
- \( (-1 000) \div (-8)\)
- \( (-100) \div (-25)\)
- \( 100 \div (-25)\)
- \( 1 000 \div (-125)\)
When two numbers are multiplied, for example \(30 \times 4 = 120\), the word "product" can be used in various ways to describe the situation:
- An expression that specifies multiplication only, such as \(30 \times 4\), is called a product or a product expression.
- The answer obtained is also called the product of the two numbers. For example, 120 is called the product of 30 and 4.
An expression that specifies division only, such as \(30 \div 5\), is called a quotient or a quotient expression. The answer obtained is also called the quotient of the two numbers. For example, 6 is called the quotient of 30 and 5.
- In each case, state whether you agree or disagree with the statement, and give an example to illustrate your answer.
- The quotient of a positive and a negative integer is negative.
- The quotient of a positive and a positive integer is negative.
- The quotient of a negative and a negative integer is negative.
- The quotient of a negative and a negative integer is positive.
- The quotient of a positive and a negative integer is negative.
- Do the necessary calculations to enable you to provide the values of the quotients.
- \((-500) \div (-20)\)
- \((-144) \div 6\)
- \(1 440 \div (-60)\)
- \((-1 440) \div (-6)\)
- \(-14 400 \div 600\)
- \(500 \div (-20)\)
- \((-500) \div (-20)\)
The associative properties of operations with integers
Multiplication of whole numbers is associative. This means that in a product with several factors, the factors can be placed in any sequence, and the calculations can be performed in any sequence. For example, the following sequences of calculations will all produce the same answer:
- \(2 \times 3\), the answer of \(2 \times 3\) multiplied by 5, the new answer multiplied by 10
- \(2 \times 5\), the answer of \(2 \times 5\) multiplied by 10, the new answer multiplied by 3
- \(10 \times 5\), the answer of \(10 \times 5\) multiplied by 3, the new answer multiplied by 2
- \(3 \times 5\), the answer of \(3 \times 5\) multiplied by 2, the new answer multiplied by 10
- Do the four sets of calculations given in A to D to check whether they really produce the same answers.
-
-
- If the numbers 3 and 10 in the calculation sequences A, B, C and D are replaced with -3 and -10, do you think the four answers will still be the same?
- Investigate, to check your expectation.
- If the numbers 3 and 10 in the calculation sequences A, B, C and D are replaced with -3 and -10, do you think the four answers will still be the same?
Multiplication with integers is associative.
The calculation sequence A can be represented in symbols in only two ways:
- \(2 \times 3 \times 5 \times 10\). The convention to work from left to right unless otherwise indicated with brackets ensures that this representation corresponds to A.
- \(5 \times (2 \times 3) \times 10\), where brackets are used to indicate that \(2 \times 3\) should be calculated first. When brackets are used, there are different possibilities to describe the same sequence.
- Express the calculation sequences B, C and D given above symbolically, without using brackets.
- Investigate, in the same way that you did for multiplication in question 2, whether addition with integers is associative. Use sequences of four integers.
-
- Calculate: \(80 - 30 + 40 - 20\)
- Calculate: \(80 + (-30) + 40 + (-20)\)
- Calculate: \(30 - 80 + 20 - 40\)
- Calculate: \((-30) + 80 + (- 20) + 40\)
- Calculate: \(20 + 30 - 40 - 80\)
- Calculate: \(80 - 30 + 40 - 20\)
Mixed calculations with integers
- Calculate.
- \(-3 \times 4 + (-7) \times 9\)
- \(-20(-4 - 7)\)
- \(20 \times (-5) - 30 \times 7\)
- \(-9(20 - 15)\)
- \(-8 \times (-6) - 8 \times 3\)
- \((-26 - 13) \div (-3)\)
- \(-15 \times (-2) + (-15) \div (-3)\)
- \(-15(2 - 3)\)
- \( (-5 + -3) \times 7\)
- \(-5 \times (-3 + 7) + 20 \div (-4)\)
- \(-3 \times 4 + (-7) \times 9\)
- Calculate.
- \(20 \times (-15 + 6) - 5 \times (-2 - 8) - 3 \times (-3 - 8)\)
- \(40 \times (7 + 12 - 9) + 25 \div (-5) - 5 \div 5\)
- \(-50(20 - 25) + 30(-10 + 7) - 20(-16 + 12)\)
- \(-5 \times (-3 + 12 - 9)\)
- \( -4 \times (30 - 50) + 7 \times (40 - 70) - 10 \times (60 - 100)\)
- \( -3 \times (-14 + 6) \times (-13 + 7) \times (-20 + 5)\)
- \( 20 \times (-5) + 10 \times (-3) + (-5) \times (-6) - (3 \times 5)\)
- \( -5(-20 - 5) + 10(-7 - 3) - 20(-15 - 5) + 30(-40 - 35)\)
- \( (-50 + 15 - 75) \div (-11) + (6 - 30 + 12) \div (-6)\)
- \(20 \times (-15 + 6) - 5 \times (-2 - 8) - 3 \times (-3 - 8)\)
Squares, cubes and roots with integers
Squares and cubes of integers
- Calculate.
- \(20 \times 20\)
- \( 20 \times (-20)\)
- \(20 \times 20\)
- Write the answers for
each of the following:
- \((-20) \times 20\)
- \((-20) \times (-20)\)
- \((-20) \times 20\)
- Complete the table.
\(x\)
1
-1
2
-2
5
-5
10
-10
\(x^2\) which is \(x \times x\)
\(x^3\)
- In each case, state for which values of \(x\), in the table in question 3, the given statement is true.
- \(x^3\) is a negative number
- \(x^2\) is a negative number
- \(x^2\) > \(x^3\)
- \(x^2\) < \(x^3\)
- \(x^3\) is a negative number
- Complete the table.
\(x\)
3
-3
4
-4
6
-6
7
-7
\(x^2\)
\(x^3\)
- Ben thinks of a number. He adds 5 to it, and his answer is 12.
- What number did he think of?
- Is there another number that would also give 12 when 5 is added to it?
- What number did he think of?
- Lebo also thinks of a number. She multiplies the number by itself and gets 25.
- What number did she think of?
- Is there more than one number that will give 25 when multiplied by itself?
- What number did she think of?
- Mary thinks of a number and calculates (the number) \(\times\) (the number) \(\times\) (the number). Her answer is 27.
What number did Mary think of?
\(10^2\) is 100 and \((-10)^2\) is also 100.
Both 10 and (-10) are called square roots of 100. 10 maybe called the posistive square root of 100> and (-10) may be called the neagtive square root of 100
- Write the positive square root and the negative square root of each number.
- 64
- 9
- 64
- Complete the table.
Number
1
4
9
16
25
36
49
64
Positive square root
3
8
Negative square root
-3
-8
- Complete the tables.
-
\(x\)
1
2
3
4
5
6
7
8
\(x^3\)
-
\(x\)
-1
-2
-3
-4
-5
-6
-7
-8
\(x^3\)
-
\(3^3\) is 27 and \((-5)^3\) is -125.
3 is called the cube root of 27, because \(3^3 = 27\).
-5 is called the cube root of -125 because \((-5)^3 = -125\).
- Complete the table.
Number
-1
8
-27
-64
-125
-216
1 000
Cube root
-3
10
The symbol \( \sqrt{}\) is used to indicate "root".
\( \sqrt[3]{-125}\) represents the cube root of -125. That means \( \sqrt[3]{-125} = -5\).
\( \sqrt[2]{36} \) represents the positive square root of 36, and \( - \sqrt[2]{36} \) represents the negative square root. The "2" that indicates "square" is normally omitted, so \( \sqrt{36} = 6\) and \( - \sqrt{36} = - 6\).
- Complete the table.
\( \sqrt[3]{-8} \)
\( \sqrt{121} \)
\( \sqrt[3]{-64} \)
\( - \sqrt{64} \)
\(\sqrt{64} \)
\( \sqrt[3]{-1} \)
\( -\sqrt{1} \)
\( \sqrt[3]{-216} \)
- Use the numbers -8, -5 and -3 to demonstrate each of the following:
- Multiplication with integers distributes over addition.
- Multiplication with integers distributes over subtraction.
- Multiplication with integers is associative.
- Addition with integers is associative.
- Multiplication with integers distributes over addition.
- Calculate each of the following without using a calculator:
- \(5 \times (-2)^3\)
- \(3 \times (-5)^2\)
- \( 2 \times (-5)^3\)
- \(10 \times (-3)^2 \)
- \(5 \times (-2)^3\)
- Use a calculator to calculate each of the following:
- \( 24 \times (-53) + (-27) \times (-34) - (-55) \times 76\)
- \( 64 \times (27 - 85) - 29 \times (-47 + 12)\)
- \( 24 \times (-53) + (-27) \times (-34) - (-55) \times 76\)
- Use a calculator to calculate each of the following:
- \(-24 \times 53 + 27 \times 34 + 55 \times 76\)
- \( 64 \times (-58) + 29 \times (47 - 12)\)
- \(-24 \times 53 + 27 \times 34 + 55 \times 76\)
If you don't get the same answers in questions 3 and 4, you have made mistakes.



