Werk met telgetalle

In hierdie hoofstuk gaan jy meer leer oor telgetalle. Jy sal leer oor verskillende maniere om telgetalle as 'n som of 'n produk uit te druk. Jy sal leer oor verskillende maniere om berekeninge te doen en verskillende maniere om jou werk neer te skryf wanneer jy berekeninge doen. Jy gaan jou vaardighede om berekeninge te doen en probleme op te los, versterk.

Hersiening

Moet glad nie 'n sakrekenaar gebruik in afdeling 1.1 nie.

Bou getalle op en breek getalle op

  1. Skryf elk van die volgende somme as een getal:

    Die woord som word gebruikom aan te dui dat twee of meer getalle bymekaargetel moet word.

    1. \( 4 000 + 800 + 60 + 5\)

    2. \( 8 000 + 300 + 7\)

    3. \( 40 000 + 9 000 + 200 + 3\)

    4. \( 800 000 + 70 000 + 3 000 + 900 + 2\)

      Die antwoord wat verkry word as die getalle bymekaar-getel word, word ook die som genoem. Ons sê: 20 is die som van 15 en 5.

    5. \( 8 \text{ duisende} + 7 \text{ honderde} + 8 \text{ ene}\)

    6. \(4 \text{ honderde duisende} + 8 \text{ ten duisende} + 4 \text{ hundreds} + 9 \text{ tiene}\)

  2. Wat is die som van \(8 000\) en \(24\)?

  3. Skryf elk van die getalle hier onder as 'n som van ene, tiene, honderde, duisende, tienduisende en honderdduisende, soos wat die getalle in vrae 1(e) en (f) gegee is.

    Wanneer 'n getal as 'n som van ene, tiene, honderde, duisende, ens. geskryf word, word dit die uitgebreide notasie genoem..

    1. \(8 706 =\)

    2. \(449 203 =\)

    3. \(83 490 = \)

    4. \(873 092 =\)

  4. Rangskik die getalle in vraag 3 van die kleinste tot die grootste.

  5. Skryf die getalle in uitgebreide notasie (byvoorbeeld \(791 = 700 + 90 + 1\)).

    1. \(493 020\)

    2. \(409 302\)

    3. \(490 032 \)

    4. \(400 932\)

  6. Rangskik die getalle in vraag 5 van die grootste tot die kleinste.

  7. Skryf elke som as een getal.

    1. \(600 000 + 40 000 + 27 000 + 100 + 20 + 34\)

    2. \(320 000 + 40 000 + 8 000 + 670 + 10 + 5 \)

    3. \( 500 000 + 280 000 + 7 000 + 300 + 170 + 38\)

    4. \( 4 \text{ honderdduisende} + 18 \text{ tienduisende} + 4 \text{ honderde} + 29 \text{ tiene} + 5 \text{ ene}\)

  8. Skryf elke som as een getal.

    1. \(300 000 + 70 000 + 6 000 + 400 + 80 + 6\)

    2. \(400 000 + 20 000 + 2 000 + 500 + 10 + 3 \)

    3. \( 500 000 + 40 000 + 7 000 + 300 + 60 + 6\)

    4. \(800 000 + 90 000 + 7 000 + 800 + 90 + 8\)

    5. \(300 000 + 110 000 + 12 000 + 400 + 110 + 3\)

  9. Tel elke keer die twee getalle bymekaar. Skryf die antwoord in uitgebreide notasie en as een getal.

    1. Die getal in 8(a) en die getal in 8(b)

    2. Die getal in 8(c) en die getal in 8(b)

    3. Die getal in 8(c) en die getal in 8(a)

    4. Die getal in 8(d) en die getal in 8(a)

    1. Trek die getal in 8(b) van die getal in 8(d) af.

    2. Is die getalle in 8(b) en 8(e) dieselfde?

    3. Trek die getal in 8(a) van die getal in 8(b) af.

  11. Skryf elk van die volgende produkte as een getal:

    Die woord produk word gebruik om aan te dui dat twee of meer getalle met mekaar vermenigvuldig moet word.

    1. \(2 \times 3\)

    2. \(2 \times 3 \times 5\)

    3. \(2 \times 3 \times 5 \times 7\)

    4. \(2 \times 3 \times 5 \times 7 \times 2\)

      Die antwoord wat verkry word as getalle met mekaar vermenigvuldig word, word ook die produk genoem. Ons sê: 20 is die produk van 2 en 10.

    5. \(2 \times 3 \times 5 \times 7 \times 2 \times 2\)

    1. Wat is die produk van 20 en 500?

    2. Skryf 1 000 as 'n produk van 5 en 'n ander getal.

    3. Skryf 1 000 as 'n produk van 50 en 'n ander getal.

    4. Skryf 1 000 as 'n produk van 25 en 'n ander getal.

    5. Wat is die produk van 2 500 en 4?

    6. Wat is die produk van 250 en 40?

  13. In die tabel hier regs word die getalle in die geel selle (blokke) gevorm deur die getal in die rooi ry bo die sel by die getal in die blou kolom links van die sel te tel. Voltooi die tabel.

    \(+\)

    2

    3

    4

    5

    10

    20

    30

    34

    40

    50

    60

    63

    65

    70

  14. Die tabel hier onder word op dieselfde manier as die tabel hier regs gevorm. Vul al die selle waarvoor jy die antwoorde dadelik weet in. Laat die ander selle vir eers oop.

    \(+\)

    8

    5

    4

    9

    7

    3

    6

    18

    36

    57

    7

    64

    3

    6

    9

    5

    8

    6

    4

Veelvoude

  1. In die rangskikking hier onder is die blou kolle in groepe soos dié: 61498.png

    Die rooi kolle is in groepe soos dié: 61514.png

    1. Hoe sal jy te werk gaan om uit te vind hoeveel blou kolle daar hier onder is as jy hulle nie een vir een wil tel nie?

    2. Volg jou plan om uit te vind hoeveel blou kolle daar is.

      61533.png 

Gestel jy wil weet hoeveel swart kolle daar in die rangskikking op bladsy 6 is. Een manier om dit vas te stel is om in groepe van drie te tel. Wanneer jy dit doen, sal jy dalk met jou vinger of potlood na die groepe moet wys terwyl jy tel sodat jy kan tred hou. Jy sal soos volg tel: drie, ses, nege, twaalf, vyftien, agtien...

'n Ander manier is om die rangskikking te ontleed en 'n paar berekeninge te doen. In die rangskikking is daar tien rye drieë van bo na onder en drie kolomme drieë van links na regs, net soos in die tabel hier regs.

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

3

Een manier om die totale getal swart kolle te berekenis om uit te werk hoeveel kolle daar in een kolom is: \(3 \times 10 = 30\); daarna werk jy uit hoeveel kolle daar in drie kolomme is: \(30 + 30 + 30 = 90\). 'n Ander manier is om uit te werk hoeveel kolle daar in een ry is: \(3 + 3 + 3 = 9\); daarna werk jy uit hoeveel kolle daar in 10 rye is: \(10 \times 9 = 90\). 'n Derde manier is om op te let dat daar \(3 \times 10 = 30\) groepe van drie is, so die totaal is \(3 \times 30 = 90\).

  1. Toe jy die getal blou kolle in vraag 1(b) bepaal het, het jy in vyfs getel, of het jy ontleed en bereken, of het jy 'n ander metode gebruik? Gebruik nou 'n ander metode om die getal blou kolle te bepaal en kyk of jy dieselfde antwoord as voorheen kry. Beskryf die metode wat jy nou gebruik.

  2. Die getalle wat jy kry as jy in vyfs tel, word veelvoude van vyf genoem. Omkring al die veelvoude van 5 in die tabel hier onder.

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    32

    33

    34

    35

    36

    37

    38

    39

    40

    41

    42

    43

    44

    45

    46

    47

    48

    49

    50

    51

    52

    53

    54

    55

    56

    57

    58

    59

    60

    61

    62

    63

    64

    65

    66

    67

    68

    69

    70

    71

    72

    73

    74

    75

    76

    77

    78

    79

    80

    81

    82

    83

    84

    85

    86

    87

    88

    89

    90

    91

    92

    93

    94

    95

    96

    97

    98

    99

    100

    101

    102

    103

    104

    105

    106

    107

    108

    109

    110

    111

    112

    113

    114

    115

    116

    117

    118

    119

    120

  3. Hoeveel rooi kolle is daar in die rangskikking op bladsy 6? Beskryf die metode wat jy gebruik om dit uit te vind.

    1. Onderstreep al die veelvoude van 7 in die tabel in vraag 3.

      'n Getal wat 'n veelvoud van 5 sowel as 'n veelvoud van 7 is, word 'n gemene veelvoud van 5 en 7 genoem.

    2. Watter veelvoude van 5 in die tabel is ook veelvoude van 7?

  5. Hoeveel geel kolle is daar in die rangskikking op bladsy 6? Beskryf die metode wat jy gebruik om dit uit te vind.

    1. Trek 'n streep deur al die veelvoude van 9 in die tabel in vraag 3.

    2. Watter getalle in die tabel in vraag 3 is gemene veelvoude van 7 en 9?

    1. Kyk na die getalle in die geel selle van die tabel hier onder. Hoe word hierdie getalle uit die getalle in die rooi ry en die getalle in die blou kolom gevorm?

    2. Vul al die selle in waarvoor jy die antwoord dadelik weet. Los die ander selle vir eers oop.

      \(\times\)

      8

      5

      4

      9

      7

      3

      6

      2

      10

      20

      7

      3

      9

      90

      5

      20

      8

      6

      4

      2

      10

      50

      20

      60

  8. Skryf die eerste dertien veelvoude van elk van die getalle in die kolom aan die linkerkant neer. Die veelvoude van 4 is reeds ingeskryf, as 'n voorbeeld.

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    2

    3

    4

    8

    12

    16

    20

    24

    28

    32

    36

    40

    44

    48

    52

    5

    6

    7

    8

    9

    10

    11

    12

    13

  9. Voltooi hierdie tabel. Jy sal dalk jou tabel van veelvoude hier bo nuttig vind vir party selle.

    \(\times\)

    6

    5

    7

    9

    4

    5

    3

    8

    10

    50

    8

    6

    7

    9

    5

    3

    4

    2

  10. Gaan terug na die tabel in vraag 8(b). As jy die getalle in party van die oop spasies nou maklik kan invul, doen dit.

  11. Gestel daar is 10 klein swart kolletjies op elk van die geel kolle in die rangskikking op bladsy 6. Hoeveel klein swart kolletjies sal daar altesaam op al die geel kolle in die rangskikking op bladsy 6 wees?

    61851.png

Veelvoude van en

  1. Hoeveel geel kolle met swart kolletjies is daar op bladsy 11? Verduidelik wat jy gedoen het om dit uit te vind.

  2. Hoeveel leerders is daar in jou klas?

    Gestel elke leerder in die klas het 'n boek soos hierdie een. Hoeveel geel kolle met swart kolletjies is daar op dieselfde bladsy (d.w.s. op bladsy 11) van al hierdie boeke saam?

  3. Elke geel kol het 10 klein swart kolletjies, soos jy op hierdie vergrote prent kan sien.

    61899.png

    1. Hoeveel klein swart kolletjies is daar op bladsy 11?

    2. Hoeveel klein swart kolletjies is daar op bladsy 11 in al die boeke in jou klas?

  4. Hier regs is 'n baie groot vergroting van een van die swartkolletjies op die geel kolle. Daar is 10 baie klein wit kolletjies op elke klein swart kolletjie. Hoeveel baie klein wit kolletjies is daar altesaam op al die swart kolletjies op bladsy 11?

    61944.png

    1. Hoeveel baie klein wit kolletjies is daar op 10 bladsye soos bladsy 11?

    2. Hoeveel baie klein wit kolletjies is daar op 100 bladsye soos bladsy 11?

10 tiene is 'n honderd: \(10 \times 10 = 100\)

10 honderde is 'n duisend: \(10 \times 100 = 1 000\)

10 duisende is 'n tienduisend: \(10 \times 1 000 = 10 000\)

10 tienduisende is 'n honderdduisend: \(10 \times 10 000 = 100 000\)

10 honderdduisende is 'n miljoen: \(10 \times 100 000 = 1 000 000\)

62130.png

    1. Skryf \(7 000 + 600 + 80 + 4\) as een getal.

    2. Skryf 10 maal die getal in (a) in uitgebreide notasie en as een getal.

    3. Skryf 100 maal die getal in (a) in uitgebreide notasie en as een getal.

  2. Skryf elk van die volgende getalle in uitgebreide notasie:

    1. 746

    2. 7 460

    3. 74 600

    4. 746 000

    5. 7 460 000

    1. Skryf 10 000 as 'n produk van 10 en een ander getal.

    2. Skryf 10 000 as 'n produk van 100 en een ander getal.

    3. Skryf 100 000 as 'n produk van 10 en een ander getal.

    4. Skryf 100 000 as 'n produk van 1 000 en een ander getal.

    5. Skryf 1 000 000 as 'n produk van 1 000 en een ander getal.

  4. Vul al die selle waarvoor jy die antwoorde dadelik weet, in hierdie tabel in. Los die ander selle vir eers oop.

    \(\times\)

    10

    20

    30

    40

    50

    60

    70

    80

    90

    100

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

  5. Vul al die selle waarvoor jy die antwoorde dadelik weet, in hierdie tabel in. Los die ander selle vir eers oop.

    \(\times\)

    100

    200

    300

    400

    500

    600

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

  6. Hoeveel veelvoude van 10 is kleiner as 250? Skat eers en skryf dan die veelvoude neer om jou skatting te kontroleer.

    1. Skatting:

    2. Kontrole:

  7. Skat eers die getal veelvoude wat gevra word, skryf hulle dan neer en tel hulle om te toets of jou skatting reg was.

    1. Hoeveel veelvoude van 100 is kleiner as 2 500?

    2. Hoeveel veelvoude van 250 is kleiner as 2 500?

    3. Hoeveel getalle kleiner as 2 500 is veelvoude van beide 100 en 250?

    4. Hoeveel getalle kleiner as 2 500 is veelvoude van beide 250 en 400?

  8. In elk van die blikkies hier onder is daar drie R10-note, drie R20-note, drie R100-note en drie R200-note.

    62382.png 

    Zain wil weet wat die totale waarde van al die R10-note in al die blikkies is. Hy besluit om dit uit te vind deur in 30's te tel, so hy sê: dertig, sestig, negentig . . . en so aan terwyl hy na een blikkie na die ander wys.

    1. Voltooi wat Zain begin doen het.

    2. Tel in 300'e om uit te vind wat die totale waarde van al die R100-note in al die blikkies is.

    1. Hoeveel geld is daar altesaam in die agt geel blikkies in vraag 13?
    2. Sit by twee klasmaats en verduidelik aan hulle hoe jy te werk gegaan het om die totale bedrag geld te bepaal.
    1. Ondersoek watter een van die volgende die maklikste vir jou is: om in twintigs tot 500 te tel of om in dertigs tot 500 te tel of om in vyftigs tot 500 te tel.
    2. Baie mense vind dit makliker om in vyftigs as in dertigs te tel. Waarom dink jy is dit so?

  11. Wat verwag jy sal die moeilikste wees: om in veertigs of in sewentigs of in negentigs te tel? Ondersoek dit en skryf 'n kort verslag.

Hier is raad wat dit makliker kan maak om in sekere teleenhede, byvoorbeeld in sewentigs, te tel.

Dit voel makliker om in vyftigs as in sewentigs te tel want jy kom by elke tweede stap by 'n veelvoud van 100 uit:

vyftig, honderd, eenhonderd en vyftig, tweehonderd, tweehonderd en vyftig, 300,

350, 400, 450, 500 ... en so aan.

Dit gebeur nie wanneer jy in sewentigs tel nie:

sewentig, eenhonderd en veertig, tweehonderd en tien, tweehonderd en tagtig ...

Dit kan jou help as jy elke keer in twee stappe oor die veelvoude van 100 gaan:

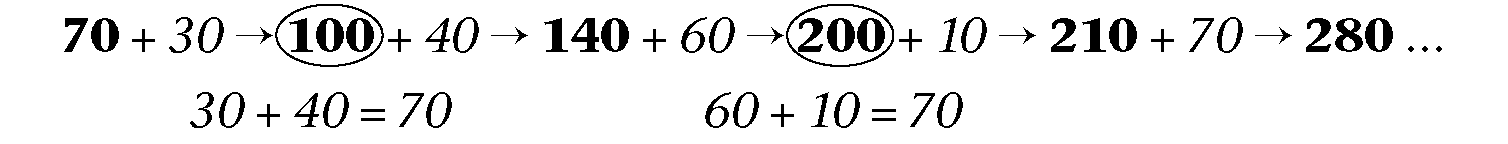
Maths_English_LG_gr7_term1-web-resources/image/Maths_English_term1_p14.png

Op dié manier word die veelvoude van 100 vir jou soos "trapklippies" terwyl jy tel.

    1. Tel in veertigs tot by 1 000. Probeer om veelvoude van 100 as trapklippies te gebruik. Jy kan die getalle hier onder neerskryf soos wat jy tel.

    2. Skryf die eerste twintig veelvoude van 80 neer.

    3. Skryf die eerste twintig veelvoude van 90 neer.

    4. Skryf die eerste tien veelvoude van 700 neer.

  2. Voltooi hierdie tabel.

    \(\times\)

    60

    50

    70

    90

    40

    20

    30

    80

    8

    6

    7

    9

    5

    3

    4

    2

    70

    30

    60

    80

    40

    90

    50

    20

Verdubbeling en halvering

  1. Skryf die volgende agt getalle in elke patroon neer:

    1. 1, 2, 4, 8, 16, 32

    2. 3 , 6, 12, 24

    3. 5, 10, 20, 40

    4. 5, 10, 15, 20

    5. 6, 12, 24, 48

  2. Watter patroon of patrone in vraag 1 word nie deur herhaalde verdubbeling gevorm nie?

    Die patroon 3 6 12 24 48 ... kan die herhaalde verdubbelingspatroon wat met 3 begin, genoem word.

  3. Skryf die eerste nege getalle van die herhaalde verdubbelingspatroon wat met die getalle in die linkerkantse kolom begin. Die patroon vir 13 is as 'n voorbeeld gegee.

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    26

    52

    104

    208

    416

    832

    1 664

    3 328

    14

    15

    16

    17

    18

    19

Verdubbeling kan gebruik word om vermenigvuldiging te doen.

Byvoorbeeld, \(29 \times 8\) kan soos volg bereken word:

8 verdubbel is 16, so \(16 = 2 \times 8\) (stap 1)

16 verdubbel is 32, so \(32 = 4 \times 8\) (stap 2)

32 verdubbel is 64, so \(64 = 8 \times 8\) (stap 3)

64 verdubbel is 128, so \(128 = 16 \times 8\) (stap 4). Verdere verdubbeling gaan verby \(29 \times 8\).

\(16 \times 8 + 8 \times 8 + 4 \times 8 = (16 + 8 + 4) \times 8 = 28 \times 8\).

So \(28 \times 8 = 128 + 64 + 32\) wat gelyk is aan 224. Dus is \(29 \times 8 = 224 + 8 = 232\).

  1. Werk soos in die voorbeeld hier bo gedoen om elk van die volgende te bereken. Skryf slegs dit neer wat jy nodig vind om neer te skryf.

    1. \(37 \times 21\)

    2. \( 17 \times 41\)

  2. Voltooi die herhaalde halveringspatrone:

    1. 1 024, 512, 256, 128

    2. 64 000, 32 000, 16 000, 8 000

Halvering kan ook gebruik word om vermenigvuldiging te doen.

Byvoorbeeld, \(37 \times 28\) kan soos volg bereken word:

\(100 \times 28 = 2 800\). Die helfte daarvan is \(50 \times 28\), wat die helfte van 2 800 is, dit wil sê 1 400.

Die helfte van \(50 \times 28\) is die helfte van 1 400, so \(25 \times 28\) is 700.

\(10 \times 28 = 280\), so \(25 \times 28 + 10 \times 28 = 980\), so \(35 \times 28 = 980\).

\(2 \times 28 = 2 \times 25 + 2 \times 3 = 56\), so \(37 \times 28\) is \(980 + 56 = 1 036\).

  1. \(80 \times 78 = 6 240\). Gebruik die inligting om elk van die volgende te bereken:

    1. \(20 \times 78\)

    2. \(37 \times 78\)

Hoeveel hoenders kan jy met R2 400 koop, as die hoenders R27 elk kos? 'n Manier om halvering te gebruik om dit te uit te werk, word op die volgende bladsy gewys.

100 hoenders kos \(100 \times 27 = \text{R}2 700\). Dit is meer as R2 400. 50 hoenders kos die helfte daarvan: R1 350.

Ek kan dus 50 hoenders of selfs meer koop.

Die helfte van 50 is 25; die helfte van R1 350 is R675.

Dus kos 75 hoenders \(\text{R}1 350 + \text{R}675 = \text{R}2 025\). Daar bly dus R375 oor.

10 hoenders kos R270, so 85 hoenders kos R2 025 + R270 = R2 295. Daar bly R105 oor.

3 hoenders kos \(3 \times \text{R}25 + 3 \times \text{R}2 = \text{R}81\).

Ek kan 88 hoenders koop. Dit sal R2 376 kos.

Koste

Redenasie

100

R2 700

50

R1 350

helfte van R2 700

25

R675

helfte van R1 350

75

R2 025

50 + 25 hoenders

10

R270

10 \(\times\) R27

85

R2 295

75 + 10 hoenders

3

R81

3 \(\times\) R27.

88

R2 376

85 + 3 hoenders

  1. Maak gebruik van halvering om uit te werk hoeveel boeke ’n skool met R5 000 kan koop, as die boeke R67 elk kos.

    Koste

    Redenasie

Vermenigvuldig om te deel

  1. R7 500 moet tussen 27 netbalspelers verdeel word. Die geld is in R10-note en daar is nie kleingeld beskikbaar nie.

    1. Hoeveel geld sal gebruik word om vir elke speler R100 te gee?

    2. Dink jy daar is genoeg geld om vir elke speler R200 te gee?

    3. Dink jy daar is genoeg geld om vir elke speler R300 te gee?

    4. Hoeveel van die R7 500 sal oor wees as elke speler R200 ontvang?

    5. Is daar genoeg geld oor om vir elke speler nog R50 te gee, dus R250 vir elkeen?

    6. Wat is die hoogste bedrag wat vir elke speler gegee kan word sodat minder as R270 oor is? Onthou dat jy nie die R10-note in kleingeld kan opbreek nie.

  2. Werk soos in vraag 1 gedoen om hierdie probleem op te los:

    Daar is 4 580 m tou op ’n groot rol. Hoeveel stukke van 17 m elk kan uit hierdie rol gesny word?

    Wenk : Jy kan begin deur vir jouself te vra hoeveel tou jy sal gebruik as jy 100 stukke van 17 m elk afsny.

  3. Werk soos in vrae 1 en 2 gedoen om hierdie probleem op te los:

    A’n Winkeleienaar het R1 800 beskikbaar waarmee hy hoenders by ’n boer kan koop. Die boer wil R26 vir elke hoender hó. Hoeveel hoenders kan die winkeleienaar koop?

Wat jy eintlik in vrae 1, 2 en 3 gedoen het, was om \(7 500 \div 27\), \(4 580 \div 17\) en \(1 800 \div 26\) te bereken. Jy het delingsprobleme opgelos. Maar die meeste van die werk was om te vermenigvuldig en dan het jy ook ’n bietjie afgetrek.

Toe jy \(1 800 \div 26\) in vraag 3 moes bereken, het jy jouself dalk gevra:

Waarmee moet ek 26 vermenigvuldig om so naby as moontlik aan 1 800 te kom?

Deling is die inverse van vermenigvuldiging.

Vermenigvuldiging is die inverse van deling.

Vermenigvuldiging en deling is inverse bewerkings.

Die woord inverse beteken "omgekeerde".

Orden en vergelyk telgetalle

Hoe ver kan jy tel, en hoe ver is ver?

  1. Hoe lank sal dit neem om tot by ’n miljoen te tel? Kom ons só dit neem een sekonde om elke getal te tel. Vind uit hoe lank een miljoen sekondes is. Gee jou antwoord in dae, ure en sekondes.

  2. Skryf 234 500 320 in woorde.

  3. Watter van die twee getalle is die kleiner een? Vul ’n > of < in om dit te wys.

    1. 876 243 ☐ 876 234

    2. 534 616 ☐ 543 016

    3. 701 02 1 ☐ 698 769

    4. 103 232 ☐ 99 878

  4. Plaas die getalle op die getallelyne so noukeurig as wat jy kan.

    1. 185 000; 178 000; 170 900; 180 500

      63876.png 

    2. 1 110 000; 1 102 900; 1 100 500; 1 105 050

      63890.png 

Die eerste ry in die tabel wys die gemiddelde afstande wat die planete van die Son af is. Hierdie afstande word in miljoene kilometer gegee.

Die afstande van die Son af word "gemiddelde afstande" genoem, want die planete is nie altyd dieselfde afstand van die Son af nie. Hulle wentelbane is nie sirkels nie.

Een miljoen kilometer is 1 000 000 km.

Planeet

Mercurius

Venus

Aarde

Mars

Jupiter

Saturnus

Uranus

Neptunus

Afstand van die Son af

58 miljoen km

108 miljoen km

150 miljoen km

228 miljoen km

778 miljoen km

1 427 miljoen km

2 870 miljoen km

4 497 miljoen km

Middellyn by die ewenaar

4 880 km

12 102 km

12 756 km

6 794 km

142 800 km

120 000 km

52 400 km

49 500 km

Die inligting in die tabel word ook in die illustrasies op bladsy 2 gegee. Bestudeer die boonste tekening om uit te vind wat "middellyn by die ewenaar" beteken.

  1. Watter planeet is die tweede verste planeet van die Son af?

  2. Hoe vergelyk Mars se afstand van die Son af met dié van Venus? Gee twee moontlike antwoorde.

  3. Rangskik die planete van die kleinste tot die grootste.

Soms hoef ons nie te weet wat die presiese getal of presiese bedrag is nie. Ons sê 'n brood kos omtrent R10, of 'n pakkie mieliemeel kos omtrent R20. Die brood kan R8 of R12 kos maar dit is naby aan R10. Die mieliemeel kan R18 of R21 kos maar dit is naby aan R20.

Wanneer jy in 'n koerant lees dat daar 15 000 toeskouers by 'n sokkerwedstryd was, weet jy dit is nie die presiese getal nie. In wiskundige taal noem ons hierdie proses afronding.

Afronding tot en

Om tot die naaste 5 af te rond, rond ons getalle wat op 1 of 2, of 6 of 7 eindig ondertoe af tot die naaste veelvoud van 5. Ons rond getalle wat op 3 of 4, of 8 of 9 eindig boontoe af tot die naaste veelvoud van 5.

Byvoorbeeld, 233 word ondertoe afgerond tot 230; 234 word boontoe afgerond tot 235; 237 word ondertoe afgerond tot 235 en 238 word boontoe afgerond tot 240.

  1. Rond die volgende getalle tot die naaste 5 af deur na die ene se waardes te kyk:

    1. 612

    2. 87

    3. 454

    4. 1 328

Om tot die naaste 10 af te rond, rond ons getalle wat op 1, 2, 3 of 4 eindig ondertoe af tot die naaste veelvoud van 10 (of tiental). Ons rond getalle wat op 5, 6, 7, 8 of 9 eindig boontoe af tot die naaste veelvoud van 10.

As jy byvoorbeeld 534 tot die naaste 10 wil afrond, moet jy na die ene-syfer kyk. Die ene-syfer is 4 en dit is nader aan 0 as aan 10. Die afgeronde getal sal 530 wees.

  1. Rond die getalle tot die naaste 10 af deur na die waarde van die ene te kyk:

    1. 12

    2. 87

    3. 454

    4. 1 325

Wanneer jy tot die naaste 100 afrond, kyk jy na die laaste twee syfers van die getal. As die getal kleiner as 50 is, rond jy ondertoe af tot die laer 100. As die getal 50 of meer is, rond jy boontoe af tot die hoër 100.

  1. Voltooi die tabel.

    Rond tot die naaste 5 af

    Rond tot die naaste 10 af

    Rond tot die naaste 100 af

    681

    5 639

    5 361

    12 458

Wanneer jy tot die naaste 1 000 afrond, kyk jy na die honderde. Is die honderdewaarde minder as, gelyk aan of meer as 500? As dit minder as 500 is, rond jy ondertoe af (die duisendewaarde bly dieselfde) en as dit gelyk aan of meer as 500 is, rond jy boontoe af.

Wanneer jy tot die naaste 10 000 afrond, kyk jy na die duisende. Is die duisendewaarde minder as, gelyk aan of meer as 5 000? As dit minder as 5 000 is, rond jy ondertoe af (die tienduisendewaarde bly dieselfde) en as dit gelyk aan of meer as 5 000 is, rond jy boontoe af.

  1. Voltooi die tabel.

    Rond tot die naaste 1 000 af

    Rond tot die naaste 10 000 af

    142 389

    343 621

    356 552

    100 489

Faktore, priemgetalle en gemene veelvoude

Verskillende maniere om dieselfde getal te lewer

Die getal 80 kan gelewer word deur 4 en 20 te vermenigvuldig: \(4 \times 20 = 80\).

Die getal 80 kan ook gelewer word deur 5 en 16 te vermenigvuldig

  1. Op watter ander maniere kan 80 gelewer word deur twee getalle te vermenigvuldig?

Die getal 80 kan ook gekry word deur 2, 10 en 4 te vermenigvuldig:

\(2 \times 10 = 20\) en \(20 \times 4 = 80\) of \(10 \times 4 = 40\) en \(40 \times 2 = 80\).

Ons kan hakies gebruik om te beskryf watter berekening eerste gedoen word. So in plaas daarvan om "\(2 \times 10 = 20\) en \(20 \times 4 = 80\)" skryf, kan ons \((2 \times 10) \times 4\). In plaas daarvan om "\(10 \times 4 = 40 \) en \(40 \times 2\)" te skryf, kan ons \(2 \times (10 \times 4)\) skryf.

  1. Wys hoe die getal 80 gekry kan word deur vier getalle te vermenigvuldig. Beskryf twee maniere waarop jy dit doen: een met hakies en een sonder hakies.

  2. Wys drie verskillende maniere waarop die getal 30 gekry kan word deur twee getalle te vermenigvuldig.

    1. Kan die getal 30 gekry word deur drie telgetalle te vermenigvuldig?

      Watter drie telgetalle?

    2. Kan die getal 30 gekry word deur vier telgetalle te vermenigvuldig wat nie die getal 1 insluit nie?

      As jy "ja" geantwoord het, watter vier getalle?

Die getal 105 kan gekry word deur 3, 5 en 7 te vermenigvuldig. Ons kan dus skryf 105 = \(3 \times 5 \times 7\). Wiskundiges beskryf dit dikwels deur te sê "105 is die produk van 3, 5 en 7", of "105 kan as die produk \(3 \times 5 \times 7\)" uitgedruk word".

  1. Druk elk van die volgende getalle as 'n produk van drie getalle uit.

    1. 248

    2. 375

Die telgetalle wat vermenigvuldig word om 'n nuwe getal te lewer, word faktore van die getal genoem.

6 en 8 is byvoorbeeld faktore van 48 want \(6 \times 8 = 48\).

Maar 6 en 8 is nie die enigste getalle wat faktore van 48 is nie. 2 is ook 'n faktor van 48 want \(48 = 2 \times 24\). En 24 is 'n faktor van 48. Die getalle 3 en 16 is ook faktore van 48 want \(48 = 3 \times 16\).

  1. Gee al die verskillende maniere waarop jy 48 as 'n produk van 2 faktore kan uitdruk.

Die getal 36 kan deur \(2 \times 2 \times 3 \times 3\) gevorm word. Omdat 2 twee keer gebruik word, word dit 'n herhaalde faktor van 36 genoem. Die getal 3 is ook 'n herhaalde faktor van 36.

    1. Druk 48 as 'n produk van drie faktore uit.

    2. Druk 75 as 'n produk van drie faktore uit.

    1. Kan 36 as 'n produk van drie faktore uitgedruk word? Hoe?

    2. Kan 36 as 'n produk van vyf faktore uitgedruk word? Hoe?

  3. Druk elk van die volgende getalle as 'n produk van soveel as moontlik faktore uit, insluitend herhaalde faktore. Moenie 1 as 'n faktor gebruik nie.

    1. 300

    2. 310

    3. 320

    4. 330

    5. 340

    6. 350

Priemgetalle

  1. Druk elk van die volgende getalle as 'n produk van soveel as moontlik faktore uit, insluitend herhaalde faktore. Moenie 1 as 'n faktor gebruik nie.

    1. 36

    2. 37

    3. 38

    4. 39

    5. 40

    6. 41

    7. 42

    8. 43

    9. 44

    10. 45

    11. 46

    12. 47

    13. 48

    14. 49

  2. Watter van die getalle in vraag 1 kan nie as 'n produk van twee telgetalle uitgedruk word nie, behalwe as die produk \(1 \times\) die getal self?

    'n Getal wat nie as 'n produk van twee telgetalle uitgedruk kan word nie, behalwe as die produk \(1 \times\) die getal self, word 'n priemgetal genoem.

    1. Watter van die getalle in vraag 1 is priemgetalle?

    2. Watter getalle tussen 20 en 30 is priemgetalle?

    3. Is 11 en 17 priemgetalle?

Eratosthenes, 'n Griekse wiskundige wat lank gelede geleef het, het 'n metode ontwerp om die priemgetalle te bepaal. Die proses word "die sif van Eratosthenes" genoem.

  1. Werk op die tabel hier regs

    Volg die stappe om al die priemgetalle tot by 100 te vind.

    Stap 1: Trek 'n kruisie oor 1.

    Stap 2: Omkring 2 en trek dan 'n kruisie oor al die veelvoude van 2.

    Stap 3: Omkring 3 en trek dan 'n kruisie oor al die veelvoude van 3.

    Stap 4: Soek die volgende getal wat nog nie 'n kruisie het nie en trek 'n kruisie oor al sy veelvoude.

    Gaan so voort.

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    32

    33

    34

    35

    36

    37

    38

    39

    40

    41

    42

    43

    44

    45

    46

    47

    48

    49

    50

    51

    52

    53

    54

    55

    56

    57

    58

    59

    60

    61

    62

    63

    64

    65

    66

    67

    68

    69

    70

    71

    72

    73

    74

    75

    76

    77

    78

    79

    80

    81

    82

    83

    84

    85

    86

    87

    88

    89

    90

    91

    92

    93

    94

    95

    96

    97

    98

    99

    100

    1. Wat is die kleinste getal wat as 'n produk van drie priemgetalle gevorm kan word, as dieselfde faktor herhaal mag word?

    2. Wat is die kleinste getal wat as 'n produk van drie priemgetalle gevorm kan word, as geen herhaalde faktore toegelaat word nie?

  3. Manare het baie werk gedoen en uitgevind dat 840 as die produk van 2, 2, 2, 3, 5 en 7 gevorm kan word. Toets of Manare reg is.

Ons kan sê dat Manare die priemfaktore van 840 bepaal het, of dat Manare 840 volledig gefaktoriseer het.

Ons kan skryf:

\(2\times 2 \rightarrow 4\times 2\rightarrow 24\times 5 \rightarrow 120 \times 7 = 840. \)

  1. Drie getalle se priemfaktore word hier onder gegee. Wat is die getalle?

    1. 3, 5, 5 en 11

    2. 3, 3, 5 en 7

    3. 2, 7, 11 en 13

  2. Ondersoek met watter van die volgende stellings jy saamstem. Gee elke keer 'n rede waarom jy saamstem of nie.

    1. As 'n getal ewe is, is 2 een van sy priemfaktore.

    2. As die helfte van 'n ewe getal ook ewe is, is 2 'n herhaalde priemfaktor.

    3. As 'n getal onewe is, is 3 een van sy priemfaktore.

    4. As 'n getal op 0 of 5 eindig, is 5 een van sy priemfaktore.

Hier is 'n metode om die priemfaktore van 'n getal te bepaal:

As die getal ewe is, deel dit deur 2. As die antwoord ook ewe is, deel weer deur 2. Hou so lank as wat dit moontlik is so aan. Sodra die antwoord onewe is, deel deur 3 as dit moontlik is. Hou so lank as moontlik aan om deur 3 te deel. Probeer dan deur 5 deel. Gaan so voort deur elke keer die volgende priemgetal as deler te probeer.

  1. Vind al die priemfaktore van elk van die volgende getalle. Werk in jou oefeningboek of op 'n los vel papier, en skryf net jou antwoorde neer.

    1. 588

    2. 825

    3. 729

    4. 999

    5. 538

    6. 113

  2. Vind ten minste drie priemgetalle tussen 800 en 850.

Grootste gemene deler en kleinste gemene veelvoud

    1. Faktoriseer 195 en 385 volledig.

    2. Is 7 'n faktor van beide 195 en 385?

    3. Is 5 'n faktor van beide 195 en 385?

Wanneer 'n getal 'n faktor van twee of meer ander getalle is, word dit 'n gemeenskaplike faktor of gemene deler van die ander getalle genoem. Byvoorbeeld, die getal 5 is 'n gemene deler van 195 en 385.

Die faktore van 'n sekere getal is 2; 2; 5; 7; 7; 11 en 17. Die faktore van 'n ander getal is 2; 3; 3; 7; 7; 11; 13 and 23. Die gemene priemfaktore van hierdie twee getalle is 2; 7; 7 en 11.

Die grootste getal wat 'n faktor van twee of meer getalle is, word die grootste gemene deler (GGD) van die getalle genoem.

  1. Bepaal elke keer die GGD van die twee gegewe getalle.

    1. \(2 \times 2 \times 5 \times 7 \times 7 \times 11 \times 17\) en \(2 \times 3 \times 3 \times 7 \times 7 \times 11 \times 13 \times 23\)

    2. 24 en 40

    3. 8 en 12

    4. 12 en 20

    5. 210 en 56

  2. Skryf vyf verskillende getalle neer, buiten getal 35, wat 35 as grootste gemene deler het.

  3. Skryf die volgende sewe getalle in elke patroon neer:

    A: 12 24 36 48

    B: 15 30 45 60

Die getalle in patroon A word veelvoude van 12 genoem en dié in patroon B word veelvoude van 15 genoem. Die getalle wat in albei patrone voorkom, byvoorbeeld 60 en 120, word gemene veelvoude van 12 en 15 genoem. Die kleinste van hierdie getalle, naamlik 60, word die kleinste gemene veelvoud (KGV) van 12 en 15 genoem.

  1. Hou aan om veelvoude van 18 en 24 neer te skryf totdat jy die KGV vind.

    1. 18 36

    2. 24 48

  2. Bepaal elke keer die GGD en KGV van die twee gegewe getalle.

    1. 5 en 7

    2. 15 en 14

    3. 20 en 30

    4. 10 en 100

    5. 8 en 9

    6. 25 en 24

    7. 8 en 12

    8. 10 en 18

Eienskappe van bewerkings

Volgorde van bewerkings en die groeperingseienskap

Gestel jy wil vir iemand sê om 'n paar berekeninge te doen. Jy kan dit doen deur instruksies te skryf. Jy kan byvoorbeeld die instruksie \(200 - 130 - 30\) skryf. 'n Instruksie soos hierdie noem ons 'n numeriese uitdrukking of 'n getalsuitdrukking.

Gestel jy het die instruksie 200 - 130 - 30 vir twee mense gegee, wat ons Ben en Sara sal noem.

Dit is wat Ben doen: \(200 - 130 = 70\) en \(70 - 30 = 40\).

Dit is wat Sara doen: \(130 - 30 = 100\) en \(200 - 100 = 100\).

Om te voorkom dat mense dieselfde numeriese uitdrukking so verskillend interpreteer of verstaan, het wiskundiges die volgende ooreenkoms aangegaan en dit word oral oor die wêreld gevolg:

'n Ooreenkoms soos dié word 'n wiskundige konvensie genoem.

In 'n numeriese uitdrukking wat net optel en aftrek behels, moet die bewerkings van links na regs uitgevoer word, tensy anders aangedui op een of ander manier.

  1. Wie het hierdie konvensie in die storie hier bo gevolg, Ben of Sara?

  2. Volg die konvensie hier bo en bereken elk van die volgende:

    1. \( 8 000 + 6 000 - 3 000\)

    2. \(8 000 - 3 000 + 6 000\)

    3. \( 8 000 + 3 000 - 6 000\)

  3. Volg die konvensie hier bo en bereken elk van die volgende:

    1. \( \text{R }25 000 + \text{R }30 000 + \text{R }13 000 + \text{R }6 000\)

    2. \( \text{R }13 000 + \text{R }6 000 + \text{R }30 000 +\text{R }25 000\)

    3. \( \text{R }30 000 + \text{R }25 000 + \text{R }6 000 + \text{R }13 000 \)

Die groeperingseienskap word ook die assosiatiewe eienskap genoem.

Al jou antwoorde in vraag 3 moet dieselfde wees. As drie of meer getalle bymekaargetel word, maak die manier waarop jy die getalle groepeer geen verskil nie. Dit word die groeperingseienskap vir optel genoem. Ons sê ook: optel is assosiatief.

  1. Ondersoek of vermenigvuldiging assosiatief is. Gebruik die getalle 2, 3, 5 en 10.

  2. Wat moet by elk van die volgende getalle getel word om 100 te kry?

    73, 56, 66 , 41 , 34, 23, 88

  3. Bereken elk van die volgende. Let op dat jy die werk baie maklik kan maak deur slim te wees wanneer jy besluit wat om eerste op te tel.

    1. \(73 + 54 + 27 + 46 + 138\)

    2. \(34 + 88 + 41 + 66 + 59 + 12 + 127\)

Die omruilingseienskap van optel en vermenigvuldiging

    1. Wat is die totale koste van 20 stoele teen R250 elk?

    2. Wat is die totale koste van 250 oefeningboeke teen R20 elk?

    3. R5 000 is vir 100 handdoeke betaal. Wat is die prys vir 1 handdoek?

    4. R100 is vir 5 000 kraletjies betaal. Wat is die prys vir 1 kraletjie?

  2. Watter van die volgende berekeninge sal dieselfde antwoord gee? Merk dié wat dieselfde antwoorde sal gee met 'n ✔ en dié wat nie sal nie met 'n ✘.

    1. \(20 \times 250 \text{ and } 250 \times 20\)

    2. \(5 000 \div 100 \text{ and } 100 \div 5 000\)

    3. \( 730 + 270 \text{ and } 270 + 730 \)

    4. \(730 - 270 \text{ and } 270 - 730\)

    Die omruilingseienskap word ook die kommutatiewe eienskap genoem.

    25 + 75 en 75 + 25 het dieselfde antwoord. Dieselfde is waar vir enige ander twee getalle. Ons sê: optel is kommutatief; die getalle kan omgeruil word.

  3. Bewys elkeen van jou antwoorde met twee verskillende voorbeelde.

    1. Is aftrek kommutatief?

    2. Is vermenigvuldiging kommutatief?

    3. Is deling kommutatief?

Nog konvensies en die verspreidingseienskap

  1. Doen die volgende:

    1. Vermenigvuldig 5 met 3 en tel dan die antwoord by 20.

    2. Tel 5 by 20 en vermenigvuldig dan die antwoord met 5.

    Wiskundiges het ooreengekom dat tensy anders aangedui, vermenigvuldiging en deling voor optel en aftrek gedoen moet word. Volgens hierdie konvensie moet die uitdrukking \(20 + 5 \times 3\) verstaan word as "vermenigvuldig 5 met 3 en tel dan 20 daarby" en nie "tel 5 by 20 en vermenigvuldig dan die antwoord met 3" nie.

  2. Volg die konvensie hier bo en bereken elk van die volgende:

    1. \(500 + 20 \times 10\)

    2. \( 500 - 20 \times 10 \)

    3. \( 500 + 20 - 10 \)

    4. \( 500 - 20 + 10 \)

    5. \( 500 + 200 \div 5 \)

    6. \( 500 - 200 \div 5 \)

As sommige van jou antwoorde dieselfde is, het jy foute gemaak.

Die konvensie hier bo skep 'n probleem. Hoe kan jy die berekeninge in vraag 1(b) met 'n numeriese uitdrukking beskryf, sonder om woorde te gebruik?

Om hierdie probleem op te los, het wiskundiges ooreengekom om hakies in numeriese uitdrukkings te gebruik. Hakies word gebruik om te spesifiseer dat die bewerkings tussen hakies eerste gedoen moet word. Die numeriese uitdrukking vir 1(b) hier bo is dus \((20 + 5) \times 5\), en die antwoord is 125.

Voorbeelde

Die uitdrukking \(12 + 3 \times 5\) beteken "vermenigvuldig 3 met 5 en tel dan 12 by". Dit beteken nie "tel 3 by 12 en vermenigvuldig dan met 5" nie.

As jy wil sê "tel 3 by 12 en vermenig-vuldig dan met 5", moet die numeriese uitdrukking \(5 \times (12 + 3)\) of \((12 + 3) \times 5\) wees. Albei beteken dieselfde.

As daar geen hakies in 'n numeriese uitdrukking is nie, beteken dit dat vermenigvuldiging en deling eerste gedoen moet word, en optel en aftrek eers later. As jy wil spesifiseer dat optel of aftrek eerste gedoen moet word, moet daardie deel van die uitdrukking tussen hakies wees.

  1. Hou die verskillende wiskundige konvensies oor numeriese uitdrukkings in gedagte wanneer jy elk van die volgende bereken:

    1. \(500 + 30 \times 10 \)
    2. \( (500 + 30) \times 10\)
    3. \(100 \times 500 + 30 \)
    4. \(100 \times (500 + 30)\)

    5. \( 500 - 30 \times 10\)

    6. \( (500 - 30) \times 10\)

    7. \( 100 \times 500 - 30 \)

    8. \(100 \times (500 - 30)\)

    9. \( (200 + 300) \div 20\)

    10. \( 200 \div 20 + 300 \div 20\)

    11. \( 600 \div (20 + 30)\)

    12. \( 600 \div 20 + 600 \div 30\)

  2. Bereken die volgende:

    1. \( 50 \times (70 + 30) \)

    2. \( 50 \times 70 + 50 \times 30\)

    3. \( 50 \times (70 - 30) \)

    4. \( 50 \times 70 - 50 \times 30\)

Jou antwoorde vir 4(a) en 4(b) moet dieselfde wees.

Jou antwoorde vir 4(c) en 4(d) moet ook dieselfde wees.

  1. Moenie berekeninge A tot I hier onder doen nie. Beantwoord net hierdie vrae oor hulle. Jy gaan jou antwoorde later kontroleer.

    1. Sal A en B dieselfde antwoorde hê?

    2. Sal G en H dieselfde antwoorde hê?

    3. Sal A en D dieselfde antwoorde hê?

    4. Sal A en G dieselfde antwoorde hê?

    5. Sal A en F dieselfde antwoorde hê?

    6. Sal D en E dieselfde antwoorde hê?

    A: \(5 \times (200 + 3)\)

    B: \( 5 \times 200 + 3 \)

    C: \(5 \times 200 + 5 \times 3\)

    D: \(5 + 200 \times 3 \)

    E: \((5 + 200) \times 3 \)

    F: \((200 + 3) \times 5\)

    G: \( 5 \times 203 \)

    H: \(5 \times 100 + 5 \times 103\)

    I: \(5 \times 300 - 5 \times 70\)

  2. Doen nou berekeninge A tot I. Kontroleer dan jou die antwoorde vir vraag 5.

    A.

    B.

    C.

    D.

    E.

    F.

    G.

    H.

    I.

    1. Kies drie verskillende getalle tussen 3 en 11, en skryf hulle hier onder neer.

      Jou eerste getal:

      Jou tweede getal:

      Jou derde getal:

    2. Tel jou eerste getal by jou derde getal. Vermenigvuldig die antwoord met jou tweede getal.

    3. Vermenigvuldig jou eerste getal met jou tweede getal. Vermenigvuldig ook jou derde getal met jou tweede getal. Tel die twee antwoorde bymekaar.

    4. As jy reg gewerk het, behoort jy dieselfde antwoorde in (b) en (c) te kry. Dink jy jy sal dieselfde resultaat met getalle tussen 10 en 100, of enige ander getalle kry?

Die feit dat jou antwoorde vir berekeninge soos dié in 7(b) en 7(c) dieselfde is vir enige getalle wat jy sou kies, word die verspreidingseienskap van vermenigvuldiging oor optel genoem.

Die verspreidingseienskap word ook die distributiewe eienskap genoem.

Dit kan soos volg beskryf word:

\(\text{eerste getal} \times \text{tweede getal} + \text{eerste getal} \times \text{derde getal} \)

= \(\text{eerste getal} \times (\text{tweede getal} + \text{derde getal})\).

Dit kan beskryf word deur te sê dat vermenigvuldiging oor optel versprei.

  1. Kyk of die verspreidingseienskap waar is vir die volgende stelle getalle

    1. 100, 50 and 10

    2. enige drie getalle van jou eie keuse (jy mag hiervoor 'n sakrekenaar gebruik)

  2. Gebruik die getalle in vraag 8(a) om te ondersoek of vermenigvuldiging ook oor aftrek versprei.

Dit is nuttig dat vermenigvuldiging oor optel versprei, want dit maak dit makliker om te vermenigvuldig.

Byvoorbeeld, \(8 \times 238\) kan bereken word deur \(8 \times 200, 8 \times 30\) en \(8 \times 8\) te bereken en die antwoorde bymekaar te tel: \(8 \times 238 = 8 \times 200 + 8 \times 30 + 8 \times 8 = 1 600 + 240 + 64 = 1 904.\)

  1. Kyk of \(8 \times 238\) werklik 1 904 is deur \(238 + 238 + 238 + 238 + 238 + 238 + 238 + 238\) te bereken, of deur 'n sakrekenaar te gebruik.

Basiese bewerkings

'n optelmetode

Om twee getalle bymekaar te tel, kan die een getal onder die ander een geskryf word.

Byvoorbeeld, om \(378 539 + 46 285\) te bereken kan die een getal só onder die ander geskryf word, dat die ene onder die ene is, die tiene onder die tiene is, en so aan.

378 539

46 285

Om die getalle so te skryf het die voordeel dat

Dit maak dit moontlik om afsonderlik met elke soort deel (ene, tiene en so aan) te werk.

Ons skyrf net dit:

In jou gedagtes kan jy dít sien:

835 234

800 000

30 000

5 000

200

30

4

687 885

600 000

80 000

7 000

800

80

5

Die getalle in elke kolom kan opgetel word om 'n nuwe stel getalle te kry:

378 539

300 000

70 000

8 000

500

30

9

46 285

40 000

6 000

200

80

5

14

14

110

110

700

700

14 000

14 000

110 000

110 000

300 000

300 000

424 824

Dis maklik om die nuwe stel getalle bymekaar te tel.

Let op dat jy die stappe hier bo in enige volgorde kan doen. In plaas daarvan om met die ene te begin soos hier bo gewys word, kan jy met die honderdduisende of enige ander dele begin. Om met die ene te begin het egter 'n voordeel: dit maak dit moontlik om meer van die werk in jou kop te doen en minder te skryf, soos jy hier onder kan sien:

378 539

46 285

424 824

Om dit te doen, word net die ene-syfer 4 van die 14 in die eerste stap neergeskryf. Die 10 van die 14 word onthou en by die 30 en 80 van die tiene-kolom getel, om 120 te kry.

Ons sê die 10 word van die ene-kolom na die tiene-kolom oorgedra. Dieselfde word gedoen as die tiene-deel opgetel word om 120 te kry: net die syfer "2" word geskryf (in die tiene-kolom, so dit beteken 20), en die 100 word oorgedra na die volgende stap.

  1. Bereken elk van die volgende:

    1. \(237 847 + 87 776\)
    2. \(567 298 + 392 076\)
    3. \( 28 387 + 365 667\)

'n Munisipale bestuurder werk aan die munisipale begroting vir 'n jaar. Hy moet probeer om die totale uitgawes vir nuwe kantoortoerusting onder R800 000 te hou. Hy moet nog begroot vir rekenaars wat dringend benodig word. Dit is wat hy sover geskryf het:

74 nuwe kantoorstoele R  54 020
42 uwe rekenaarskerms R 100 800
12 nuwe drukkers R 141 600
18 nuwe teewaentjies R  25 740
8 nuwe matte vir senior personeel se kantore R 144 000
108 klein liasseerkabinette van plastiek R  52 380
'n Nuwe tafel vir die raadsaal R  48 000
18 nuwe stoele vir die raadsaal R  41 400
R ______

  1. Hoeveel het die munisipale bestuurder altesaam vir drukkers en rekenaarskerms begroot?

  2. Hoeveel, in totaal, het die munisipale bestuurder vir stoele en tafels begroot?

  3. Werk die totale koste uit van al die items waarvoor die munisipale bestuurder begroot het.

  4. Bereken

    1. 23 809 + 2 009 + 23

    2. 320 293 + 16 923 + 349 + 200 323

Aftrekmetodes

Daar is baie maniere om een getal van 'n ander af te trek. R835 234 - R687 885 kan byvoorbeeld bereken word deur van R687 885 tot R835 234 "op te vul":

\(687 885 + 15 → 687 900 + 100→688 000 + 12 000 →700 000 + 135 234→ 835 234\)

Die verskil tussen R687 885 en R835 234 kan nou bereken word deur die getalle bymekaar te tel wat by 687 885 getel moes word om 835 234 te kry.

So \(\text{R}835 234 - \text{R}687 885 = \text{R}147 349\).

15

100

12 000

135 234

147 349

'n Ander maklike manier om af te trek is om af te rond en te kompenseer. Om byvoorbeeld \(\text{R}3 224 - \text{R}1 885\) te bereken, kan die R1 885 boontoe tot R2 000 afgerond word. Die berekening kan soos volg voortgaan:

In plaas daarvan om R3 224 - R1 885 te bereken, wat 'n bietjie moeilik is, kan ons

\(\text{R}3 339 - \text{R}2 000\) bereken. Dit is maklik: \(\text{R}3 339 - \text{R}2 000 = \text{R}1 339\).

Dit beteken dat \(\text{R}3 224 - \text{R}1 885 = \text{R}1 339,\) want \(\text{R}3 224 - \text{R}1 885 = (\text{R}3 224 + \text{R}115) - (\text{R}1 885 + \text{R}115)\).

Om vraag 1 te doen, kan jy enige een van die twee metodes hier bo gebruik, of enige ander metode wat jy ken of verkies. Moenie 'n sakrekenaar gebruik nie, want die doel van hierdie werk is dat jy moet verstaan hoe getalle afgetrek word. Wat jy hier sal leer, sal jou later help om algebra te verstaan.

  1. Bereken elk van die volgende:

    1. \(6 234 - 2 992\)

    2. \(76 214 - 34 867\)

    3. \( 134 372 - 45 828 \)

    4. \(623 341 - 236 768\)

  2. Kontroleer elk van jou antwoorde in vraag 1 deur op te tel, of deur af te trek met 'n ander metode as die metode wat jy reeds gebruik het.

Nog 'n aftrekmetode is om aan die getalle in uitgebreide notasie te dink. Om byvoorbeeld \(\text{R}835 234 - \text{R}687 885\) te bereken, wat reeds op die vorige bladsy op 'n ander manier gedoen is, kan ons soos volg werk:

Ons skryf net dit:

In jou gedagtes kan jy dít sien:

835 234

800 000

30 000

5 000

200

30

4

687 885

600 000

80 000

7 000

800

80

5

Dit is ongelukkig nie nou moontlik om in die kolomme af te trek nie. Die dele van die groter getal kan egter geherrangskik word om aftrekking in elke kolom moontlik te maak:

835 234

700 000

120 000

14 000

1100

120

14

687 885

600 000

80 000

7 000

800

80

5

100 000

40 000

7 000

300

40

9

Die antwoord is nou duidelik sigbaar; dit is 147 349.

Die herrangskikking, wat ook "leen" genoem word, is soos volg gedoen: 10 is van die 30 in die tiene-kolom weggeneem en by die 4 in die ene-kolom getel. 100 is van die 200 in die honderde-kolom weggeneem en by die 20 getel wat in die tiene-kolom oorgebly het. 1 000 is van die 5 000 in die duisende-kolom weggeneem en by die 100 getel wat in die honderde-kolom oorgebly het.

  1. Beskryf die ander herrangskikkings wat in die werk hier bo gedoen is.

Dit is nie prakties om die uitgebreide notasie en die herrangskikkings te skryf elke keer wat jy aftrek nie. Met 'n bietjie oefening kan jy egter leer om dit alles in jou kop te doen. Party mense maak klein merkies bokant die syfers van die groter getal, of verander selfs die syfers, om tred te hou met die herrangskikkings wat hulle in hulle koppe doen.

835 234

687 885

147 349

  1. Bereken elke keer die verskil tussen die twee motorpryse wat gegee word:

    1. R73 463 en R88 798

    2. R63 378 en R96 889

  2. Skat eers die antwoord tot die naaste 100 000 en bereken dan.

    1. \(238 769 - 141 453\)

    2. \(856 333 - 439 878\)

  3. Skat eers die antwoord tot die naaste 10 000 en bereken dan.

    1. \(88 023 - 45 664\)

    2. \(342 029 - 176 553\)

  4. Kyk weer na die munisipale begroting op bladsy 35. Hoeveel geld het die munisipale bestuurder oor om nuwe rekenaars te koop?

  5. Bereken.

    1. \(670 034 - 299 999\)

    2. \(670 034 - 300 000\)

    3. \(376 539 - 175 998\)

    4. \(376 541 - 176 000\)

'n vermenigvuldigingsmetode

\(6 \times \text{R}3 258 \) kan in dele bereken word, soos hier gewys word.

\(6 \times \text{R}3 000 = \text{R}18 000\)

\(6 \times \text{R}200 = \text{R}1 200\)

\(6 \times \text{R}50 = \text{R}300\)

\(6 \times \text{R}8 = \text{R}48\)

3

2

5

8

\(\times\)

6

4

8

3

0

0

1

2

0

0

1

8

0

0

0

1

9

5

4

8

Die vier gedeeltelike produkte kan nou bymekaargetel word om die antwoord te kry, wat R19 548 is. Dit is gerieflik om die werk in kolomme vir ene, tiene, honderde en so aan te skryf, soos hier regs bo gewys word.

As jy bereid is om 'n bietjie meer te dink, kan jy die antwoord met selfs nog minder skryfwerk bepaal. Dit kan jy regkry deur van regs na links te werk om die gedeeltelike produkte te bereken en deur dele van die gedeeltelike antwoorde na die volgende kolom "oor te dra", net soos wat jy maak as jy van regs na links in kolomme werk. Dit werk so:

3

2

5

8

\(\times\)

6

1

9

5

4

8

Wanneer \(6 \times 8 = 48\) bereken word, word net die "8" in die ene-kolom neergeskryf. Die "4" wat 40 voorstel, word nie geskryf nie. Dit word vir die oomblik in jou kop "gebêre".

Wanneer \(6 \times 50 = 300\) bereken word, word die 40 van die vorige stap by 300 getel om 340 te kry. Weer word net die "4" wat 40 voorstel, geskryf. Die 300 word onthou of "oorgedra" om by die antwoord van die volgende stap te tel. En so hou jy aan werk.

  1. Bereken elk van die volgende. Moenie 'n sakrekenaar gebruik nie.

    1. \(8 \times 786\)

    2. \(9 \times 3 453\)

    3. \(60 \times 786\)

    4. \(60 \times 7 860\)

  2. Jy mag 'n sakrekenaar gebruik om jou antwoorde vir vraag 1 te kontroleer. Herhaal die werk as jou antwoorde nie reg is nie, sodat jy kan leer waar jy foute maak. Bêre dan weer jou sakrekenaar.

  3. Gebruik jou antwoorde vir vrae 1(a) en (c) om uit te vind hoeveel \(68 \times 786 \) is.

Om \(36 \times 378\), te bereken, kan jy die werk in twee dele opbreek, naamlik \(30 \times 378 \) en \(6 \times 378\).

  1. Bereken \(36 \times 378\).

    Die berekening, in kolomme, van \(76 \times 2 348\) is hier regs volledig uitgeskryf.

    2

    3

    4

    8

    \( \times \)

    7

    6

    A

    4

    8

    B

    2

    4

    0

    C

    1

    8

    0

    0

    D

    1

    2

    0

    0

    0

    E

    5

    6

    0

    F

    2

    8

    0

    0

    G

    2

    1

    0

    0

    0

    H

    1

    4

    0

    0

    0

    0

    1

    7

    8

    4

    4

    8

    1. Verduidelik hoe die 240 in ry B gekry is.

    2. Verduidelik hoe die 560 in ry E gekry is.

    3. Verduidelik hoe die 21 000 in ry G gekry is.

    'n Korter weergawe van die berekening van \(76 \times 2 348\) in kolomme word hier regs gewys.

    2

    3

    4

    8

    \(\times\)

    7

    6

    1

    4

    0

    8

    8

    1

    6

    4

    3

    6

    0

    1

    7

    8

    4

    4

    8

    Jy kan probeer om die berekeninge in vraag 6 op hierdie manier te doen. As dit vir jou moeilik is, kan jy eers party van hulle volledig uitskryf en dan probeer om minder te skryf wanneer jy vermenigvuldig.

  3. Bereken elk van die volgende.

    1. \(53 \times 738 \)

    2. \(73 \times 3 457\)

  4. Bereken.

    1. \(64 \times 3 478 \)

    2. \( 78 \times 1 298\)

    3. \(37 \times 3 428\)

    4. \(78 \times 7 285\)

  5. Gebruik 'n sakrekenaar om jou antwoorde vir vraag 7 te kontroleer. Doen die vrae wat jy verkeerd gehad het oor sodat jy kan leer om reg te werk.

  6. Gebruik jou korrekte antwoorde vir vraag 7 om die antwoorde vir die volgende te gee, sonder om enige berekeninge te doen:

    1. \( 101 244 \div 1 298\)

    2. \( 568 230 \div 7 285\)

  7. Bereken, sonder om 'n sakrekenaar te gebruik.

    1. \( 3 659 \times 38 \)

    2. \(27 \times 23 487 \)

    3. \( 486 \times 278\)

    4. \(2 135 \times 232\)

'n proses wat langdeling genoem word

Jy mag 'n sakrekenaar gebruik om vrae 1 tot 6 te doen.

  1. Jy wil lewende hoenders teen R37 elk koop en jy het R920 beskikbaar.

    Hoeveel lewende hoenders kan jy daarmee koop?

  2. R880 moet gelykop tussen 34 leerders verdeel word.

    Hoeveel volle rande kan elke leerder kry?

  3. Jy wil lewende hoenders teen R47 elk koop. Jy het R1 280 beskikbaar. Hoeveel lewende hoenders kan jy koop?

  4. 42 sakkies rys wat ewe veel weeg, weeg saam 7 560 g. Hoeveel weeg een sakkie?

  5. Die skets hier regs is 'n akkurate skets van die agterkant van 'n huis. Die rooi lyn op die skets is 70 mm lank en dit wys die breedte van die huis. Die blou lyn op die skets dui die hoogte van die skoorsteen aan. Moenie nou al die blou lyn meet nie.

    Die breedte van die werklike huis is 5 600 mm, en die hoogte van die skoorsteen is 3 360 mm.

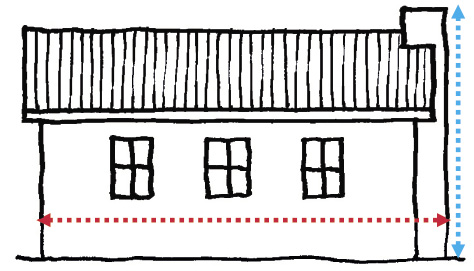
    Maths_English_LG_gr7_term1-web-resources/image/MathsA%20Grade%207% 20Chapter_opt.jpeg
    1. Hoeveel keer is die huis groter as die skets? Beskryf wat jy kan doen om dit uit te vind.

    2. Bereken hoe lank die blou lyn op die skets moet wees.

    3. Meet nou die blou lyn om jou antwoord vir (b) te kontroleer.

    Deling kan vir verskillende doeleindes gebruik word:

    In vraag 1 het jy geweet die bedrag is in gelyke dele verdeel. Jy moes uitvind hoeveel dele daar is (hoeveel hoenders). Dit word groepering genoem. In vraag 2 het jy geweet die bedrag is in 34 gelyke dele verdeel. Jy moes uitvind hoe groot elke deel is (hoeveel geld elke leerder sal kry). Dit word verdeling genoem.

    1. Wat vereis vraag 3, verdeling of groepering?

    2. Wat vereis vraag 4, verdeling of groepering?

    In vraag 6 is deling vir 'n ander doel as verdeling of groepering gedoen.

    Bêre nou jou sakrekenaar. Dit is baie belangrik om delingsprobleme in jou kop te kan doen. Die aktiwiteite wat volg sal jou help om dit beter as voorheen te doen. Terwyl jy aan hierdie aktiwiteite werk, sal jy dikwels die produk van twee getalle moet skat. As jy produkte goed kan skat, raak deling makliker om te doen. So, om te begin, doen vraag 8, wat vir jou geleenthede sal gee om jou vaardigheid om produkte te skat te oefen.

    1. Wat dink jy is die naaste aan 4 080:

      \(10 \times 74 \) of \( 30 \times 74\) of \(50 \times 74\) of \(70 \times 74\) of \( 90 \times 74 \)?

    2. Bereken 'n paar van die produkte om jou antwoord te kontroleer.

    3. Wat dink jy is die naaste aan \(9 238: 30 \times 38 \) of \( 50 \times 38\) of \( 100 \times 38 \) of \(150 \times 38\) of \(200 \times 38\) of \(250 \times 38\) of \(300 \times 38\)

    4. Bereken 'n paar van die produkte om jou antwoord te kontroleer.

    5. Wat dink jy is die naaste aan \(9 746: 10 \times 287\) of \(20 \times 287\)

      of \(30 \times 287 \) of \(40 \times 287\) of \( 50 \times 287\) of \(60 \times 287 \) of \(70 \times 287\)?

    6. Bereken 'n paar van die produkte om jou antwoord te kontroleer.

    7. Met watter veelvoud van 10 moet jy 27 vermenigvuldig om so naby as moontlik aan 6 487 te kom?

  9. 'n Skoolhoof wil T-hemde koop vir die 115 Graad 7-leerders in die skool. Die T-hemde kos R67 elk, en 'n bedrag van R8 500 is beskikbaar. Dink jy daar is genoeg geld om vir al die leerders T-hemde te koop? Verduidelik jou antwoord.

    1. Hoeveel sal 100 van die T-hemde kos?

    2. Hoeveel geld sal oor wees as 100 T-hemde gekoop word?

    3. Hoeveel geld sal oor wees as nog 20 T-hemde gekoop word?

Die skoolhoof wil uitwerk presies hoeveel T-hemde, teen R67 elk, sy met R8 500 kan koop. Hoe sy gedink en geskryf het word hier onder beskryf.

Stap 1

Wat sy skryf:

Wat sy dink

67

8 500

Ek wil uitvind hoeveel "groepe" van 67 daar in 8 500 is.

Stap 2

Wat sy skryf:

Wat sy dink:

100

Ek dink daar is ten minste 100 "groepe" van 67 in 8 500.

67

8 500

6 700

\(100 \times 67 = 6 700\). Ek moet weet hoeveel bly oor.

1 800

Ek wil uitvind hoeveel "groepe" van 67 daar in 1 800 is.

Stap 3 (Sy moet die een "0" van die 100 wat bo staan uitvee om plek te maak.)

Wat sy skryf:

Wat sy dink:

120

Ek dink daar is ten minste 20 "groepe" van 67 in 1 800.

67

8 500

6 700

1 800

1 340

\(20 \times 67 = 1 340\). Ek moet weet hoeveel bly oor.

460

Ek wil uitvind hoeveel "groepe" van 67 daar in 460 is.

Stap 4 (Sy vee nog 'n "0" uit.)

Wat sy skryf:

Wat sy dink:

125

Ek dink daar is ten minste 5 "groepe" van 67 in 460.

67

8 500

6 700

1 800

1 340

460

335

\(5 \times 67 = 335\). Ek moet weet hoeveel bly oor.

125

Ek wil uitvind hoeveel "groepe" van 67 daar in 125 is.

Stap 5 (Sy vee die "5" uit.)

Wat sy skryf:

Wat sy dink:

126

Ek dink daar is nog net een "groep" van 67 in 125.

67

8 500

6 700

1 800

1 340

460

335

125

67

IEk wonder hoeveel geld sal oor wees.

58

So, ons kan 126 T-hemde koop en R58 sal oor wees.

Moenie 'n sakrekenaar gebruik vir die vrae wat volg nie. Die doel van hierdie werk is dat jy 'n goeie begrip moet ontwikkel van hoe deling gedoen kan word. Kontroleer al jou antwoorde deur vermenigvuldiging te doen.

    1. Selina het 85 hoenders gekoop, almal teen dieselfde prys. Sy het altesaam R3 995 betaal. Wat het elk van die hoenders gekos? Jou eerste stap kan wees om uit te werk hoeveel Selina sou betaal het as sy R10 per hoender betaal het, maar jy kan met 'n groter stap begin as jy wil.

    2. Anton het R4 850. Hy wil 'n paar jong bokke koop. Die bokke kos R78 elk. Hoeveel bokke kan hy koop? .

  2. Bereken die volgende sonder om 'n sakrekenaar te gebruik:

    1. \( 7 234 \div 48 \)

    2. \( 3 267 \div 24\)

    3. \( 9 500 \div 364\)

    4. \( 8 347 \div 24\)

    1. ’n Sjokoladefabriek het eendag 9 325 sjokolades van ’n baie spesiale soort sjokolade gemaak. Hulle is in klein versierde boksies verpak, met 24 sjokolades per boksie. Hoeveel boksies is gevul?

    2. ’n Boer verkoop eiers, wat in houers verpak is, aan die plaaslike supermarkte. Daar is 36 eiers in een houer. Een maand het die boer 72 468 eiers aan die supermarkte verkoop. Hoeveel houers was dit?

Probleemoplossing

Koers en verhouding

Jy mag 'n sakrekenaar in hierdie afdeling gebruik.

  1. Die mense in 'n dorpie kry hulle water van 'n nabygeleë dam af. Op 'n sekere dag bevat die dam 688 000 liter water. Die mense gebruik elke dag omtrent 85 000 liter water. Hoeveel dae sal die water in die dam hou as dit nie reën nie?

    In plaas daarvan om te sê "85 000 liter elke dag" of "8 cm elke uur", sê mense dikwels "teen 'n koers van 85 000 liter per dag" of "teen 'n koers van 8 cm per uur".

  2. Gedurende 'n tydperk van baie swaar reëns styg die watervlak in 'n sekere rivier teen 'n koers van 8 cm per uur. As dit so voortgaan, met hoeveel sal die watervlak in 24 uur styg?

  3. 'n Vrou ry van Johannesburg na Durban. Haar afstand van Durban af verminder teen 'n tempo van omtrent 95 km per uur. Ongeveer hoe ver ry sy in 4 ure?

  4. Die getal werklose mense in 'n sekere provinsie vermeerder teen 'n koers van ongeveer 35 000 mense per jaar. As daar 860 000 werklose mense in die jaar 2000 was, ongeveer hoeveel werklose mense sal daar in die jaar 2020 wees?

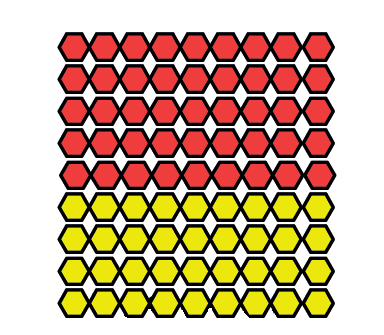
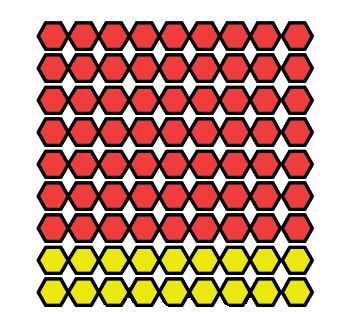
  5. In patroon A hier onder is daar 5 rooi krale vir elke 4 geel krale.

    Beskryf patroon B en patroon C op dieselfde manier.

    Maths_English_LG_gr7_term1-web-resources/image/Maths_English_term1_p47_1.png

    Patroon A

    Maths_English_LG_gr7_term1-web-resources/image/Maths_English_term1_p47_2.png

    Patroon B

    Maths_English_LG_gr7_term1-web-resources/image/Maths_English_term1_p47_3.png

    Patroon C

    In 'n sekere kosfabriek word twee masjiene gebruik om blikkies sousbone te produseer. Masjien A produseer teen 'n tempo van 800 blikkies per uur en masjien B teen 'n tempo van 2 400 blikkies per uur.

    1. Voltooi die tabel om te wys hoeveel blikkies sousbone gedurende verskillende tye deur die twee masjiene geproduseer sal word.

      Getal ure

      1

      2

      3

      5

      8

      Getal blikkies by masjien A

      800

      1 600

      2 400

      4 000

      Getal blikkies by masjien B

      2 400

      4 800

    2. Hoeveel vinniger is masjien B as masjien A?

    3. Hoeveel blikkies sal masjien B produseer in die tyd wat dit masjien A neem om 30 blikkies te produseer?

    4. Hoeveel blikkies sal masjien B produseer in die tyd wat dit masjien A neem om 200 blikkies te produseer?

    5. Hoeveel blikkies sal masjien B produseer in die tyd wat dit masjien A neem om 1 blikkie te produseer?

    Die patrone in vraag 5 kan soos volg beskryf word:

    In patroon A is die verhouding van geel krale tot rooi krale 4 tot 5. Dit word geskryf as 4 : 5.

    In patroon B is die verhouding tussen geel krale en rooi krale 3 : 6, en in patroon C is die verhouding 2 : 7. In vraag 6 maak masjien A 1 blikkie vir elke 3 blikkies wat masjien B maak. Dit kan beskryf word deur te sê die verhouding tussen die produksietempo's van masjien A en masjien B is 1 : 3.

  7. Twee groot lorries ry baie stadig op 'n snelweg. Lorrie A ry 20 km per uur, en lorrie B ry 30 km per uur. Albei lorries ry die hele tyd teen hierdie spoed.

    1. Watter afstand sal lorrie B ry in dieselfde tyd wat lorrie A 10 km ry?

    2. In die tabel hier onder word die afstande gegee wat lorrie A in sekere tye ry. Voltooi die tabel om die afstande te wys wat lorrie B in dieselfde tydperke ry.

      Afstand deur lorrie A gery

      10 km

      18 km

      50 km

      100 km

      30 km

      Afstand deur lorrie B gery

    3. Watter afstand sal lorrie B ry in dieselfde tyd wat lorrie A 1 km ry?

    4. Wat is die verhouding tussen die spoed waarteen lorrie A ry en die spoed waarteen lorrie B ry?

  8. R240 sal in die verhouding 3 : 5 tussen David en Sally gedeel word. Dit beteken Sally kry R5 vir elke R3 wat David kry. Hoeveel sal David en Sally elkeen in totaal kry?

  9. Hoeveel sal elkeen kry as R14 400 op elk van die volgende maniere tussen twee mense verdeel word?

    1. In die verhouding 1 : 3

    2. In die verhouding 5 : 7

Finansiële wiskunde

'n Man leen R12 000 by 'n bank vir een jaar. Hy moet 15% rente aan die bank betaal. Dit beteken dat hy, afgesien van die R12 000 wat hy na 'n jaar aan die bank moet terugbetaal, ook 15 honderdstes van R12 000 moet betaal vir die voorreg om die geld te gebruik wat eintlik aan die bank behoort.

15% word as 15 persent gelees en dit is net 'n ander manier om 15 honderdstes te sê.

Een honderdste van R12 000 kan bereken word deur R12 000 deur 100 te deel. Hierdie bedrag kan dan met 15 vermenigvuldig word om 15 honderdstes van R12 000 te bereken.

Die geld wat betaal word om iemand anders se huis te gebruik word huur genoem. Die geld wat betaal word om iemand anders se geld te gebruik word rente genoem.

Moenie 'n sakrekenaar gebruik wanneer jy die volgende vrae doen nie.

  1. Bereken \(12 000 \div 100\) en vermenigvuldig dan die antwoord met 15.

  2. Bereken:

    1. 12% van R8 000

    2. 18% van R24 000

  3. Bereken hoeveel rente betaal moet word.

    1. 'n Bedrag van R6 000 word vir 1 jaar teen 9% rente geleen.

    2. 'n Bedrag van R21 000 word vir 3 jaar teen 11% rente per jaar geleen.

    3. 'n Bedrag van R45 000 word vir 10 jaar teen 12% rente per jaar geleen.

    'n Man koop 'n motor vir R60 000 en verkoop dit vir R75 000. Die verskil van R15 000 word die wins genoem. In hierdie geval is die wins 'n kwart van R60 000, wat dieselfde as 25 honderdstes of 25% is. Dit kan beskryf word deur te sê "hy het 25% wins gemaak".

  4. 'n Handelaar koop en verkoop gebruikte voertuie. Bereken die wins.

    1. Hy koop 'n motor vir R40 000 en verkoop dit vir R52 000.

    2. Hy koop 'n vragmotor vir R100 000 en verkoop dit teen 'n wins van 28%.

    3. Hy koop 'n bakkie vir R120 000 en verkoop dit teen 'n wins van 30%.

    'n Winkelier het 'n stoof vir R2 000 aangekoop en dit vir R1 600 verkoop. Die winkelier het nie wins gemaak nie; hy het die stoof teen 'n verlies van R400 verkoop.

    1. Hoeveel is 1 honderdste van R2 000?

    2. Hoeveel honderdstes van R2 000 is R400?

    3. Hoeveel is 20% van R2 000?

    Let op dat jy in vraag 5(b) uitgewerk het teen watter persentasie verlies die winkelier die stoof verkoop het.

  6. ie winkelier het ook 'n yskas, wat gewoonlik vir R4 000 verkoop word, teen 'n afslag van 20% verkoop. Dit beteken die klant het 20% minder as die gewone prys betaal. Bereken die afslag in rand en die bedrag wat die klant vir die yskas betaal het.